Post

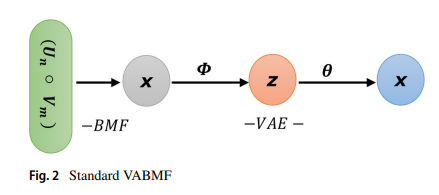
VABMF

Posted
Preview Image
By jayarnim
4 min read

Previous Research

  • 선형 행렬분해 기반 잠재요인 모형(Latent Factor Model based on Linear Matrix Factorization) : 상호작용의 비선형 특징을 포착하지 못함

    \[\hat{r}_{u,i}=\overrightarrow{\mathbf{p}}_{u} \cdot \overrightarrow{\mathbf{q}}_{i}^{T}\]

  • 비선형 행렬분해 기반 잠재요인 모형(Latent Factor Model based on Non-Linear Matrix Factorization) : 상호작용 데이터의 희박함에 따른 정보 불확실성을 반영하지 아니함

    \[\hat{r}_{u,i}=\text{MLP}\left[\overrightarrow{\mathbf{p}}_{u} \oplus \overrightarrow{\mathbf{q}}_{i}\right]\]

  • 베이지안 행렬분해 기반 잠재요인 모형(Latent Factor Model based on Bayesian Matrix Factorization)

    • 확률적 행렬분해(Probabilistic Matrix Factorization; PMF) : 학습파라미터를 추정함에 있어서 그 사후 확률 분포를 추정하지 아니하고 최대사후확률(Maximum a Posteriori; MAP) 추정치로 점 추정하므로 실질적으로는 정보 불확실성을 반영한다고 볼 수 없음

      \[\begin{aligned} \mathbf{R} \mid \mathbf{U},\mathbf{V} &\sim \mathcal{N}\left(\mathbf{U}\mathbf{V}^{T}, \sigma^{2}\right)\\ \mathbf{U} &\sim \mathcal{N}\left(\overrightarrow{\mu}_{U}, \lambda_{U}^{-1}\cdot\mathbf{I}\right)\\ \mathbf{V} &\sim \mathcal{N}\left(\overrightarrow{\mu}_{V}, \lambda_{V}^{-1}\cdot\mathbf{I}\right) \end{aligned}\]

    • 베이지안 확률적 행렬분해(Bayesian Probabilistic Matrix Factorization; BPMF) : 학습파라미터의 사후 확률 분포를 추정하나 MCMC를 활용하기에 학습 속도가 현저히 느림

      \[\begin{aligned} \mathbf{R} \mid \mathbf{U},\mathbf{V} &\sim \mathcal{N}\left(\mathbf{U}\mathbf{V}^{T}, \sigma^{2}\right)\\ \mathbf{U} \mid \overrightarrow{\mu}_{U},\Lambda_{U} &\sim \mathcal{N}\left(\overrightarrow{\mu}_{U},\Lambda_{U}\right)\\ \overrightarrow{\mu}_{U} ; \Lambda_{U} &\sim \mathcal{N}\left(\mu_{0}, (\beta_{0} \cdot \Lambda_{U})^{-1}\right)\\ \Lambda_{U} &\sim \mathcal{W}\left(\mathbf{W}_{0}, \nu_{0}\right)\\ \mathbf{V} \mid \overrightarrow{\mu}_{V},\Lambda_{V} &\sim \mathcal{N}\left(\overrightarrow{\mu}_{V},\Lambda_{V}\right)\\ \overrightarrow{\mu}_{V} ; \Lambda_{V} &\sim \mathcal{N}\left(\mu_{0}, (\beta_{0} \cdot \Lambda_{V})^{-1}\right)\\ \Lambda_{V} &\sim \mathcal{W}\left(\mathbf{W}_{0}, \nu_{0}\right) \end{aligned}\]

VABMF

  • VABMF(Variational AutoEncoder Bayesian Matrix Factorization) : 베이지안 행렬분해와 변분 오토인코더를 결합하여 선형적 잠재요인 및 비선형적 잠재요인의 불확실성을 모델링하는 잠재요인 모형

    01

    • Linear Matrix Factorization : 사용자 벡터와 아이템 벡터 간 선형 상호작용 포착
    • AutoEncoder : 사용자 벡터와 아이템 벡터 간 비선형 상호작용 포착
    • Serial Combination : 희소성이 높은 원형 $\mathbf{R}$ 이 아니라 그 근사값 $\mathbf{X}=\mathbf{U} \cdot \mathbf{V}$ 을 복원함으로써 계산 효율성 향상
    • Bayesian Approach : 상호작용 데이터의 희박함에 따른 학습파라미터의 정보 불확실성 반영
    • Variational Inference : 사후 확률 학습 과정 상의 효율성 향상

  • Annotation

    • $i = 1,2,\cdots,M$ : User Index
    • $j = 1,2,\cdots,N$ : Item Index
    • $K$ : Dimension of Latent Factors
    • \(r_{i,j} \in \mathbf{R}_{M \times N}\) : User-Item Interaction Matrix
    • \(x_{i,j} \in \mathbf{X}_{M \times N}\) : User-Item Latent Matrix
    • Params of Bayesian Matrix Factorization
      • \(\overrightarrow{\mathbf{u}}_{i} \in \mathbf{U}_{M \times K}\) : User-Linear Latent Factor Matrix
      • \(\overrightarrow{\mathbf{v}}_{j} \in \mathbf{V}_{N \times K}\) : Item-Linear Latent Factor Matrix
    • Params of Variational AutoEncoder
      • \(\overrightarrow{\mathbf{z}}_{j} \in \mathbf{Z}_{N \times K}\) : Item-NonLinear Latent Factor Matrix
      • $\Phi$ : Encoder Params
      • $\Theta$ : Decoder Params

Part.1 Bayesian Matrix Factorization

  • Prior Determination of User-Latent Factor Vector:

    \[\begin{aligned} \overrightarrow{\mathbf{u}}_{i} &\sim \mathcal{N}\left(0, \tau^{-1}\mathbf{I}_{K}\right) \end{aligned}\]

  • Prior Determination of Item-Latent Factor Vector:

    \[\begin{aligned} \overrightarrow{\mathbf{v}}_{j} &\sim \mathcal{N}\left(0, \tau^{-1}\mathbf{I}_{K}\right) \end{aligned}\]

  • Log Posterior Estimation of $\mathbf{U},\mathbf{V}$:

    \[\begin{aligned} \log{P\left(\overrightarrow{\mathbf{u}}_{i}, \overrightarrow{\mathbf{v}}_{j} \mid r_{i,j}\right)} &\propto \log{\mathcal{L}\left(r_{i,j} \mid \overrightarrow{\mathbf{u}}_{i}, \overrightarrow{\mathbf{v}}_{j}\right)} + \log{\pi\left(\overrightarrow{\mathbf{u}}_{i}\right)} + \log{\pi\left(\overrightarrow{\mathbf{v}}_{j}\right)} \end{aligned}\]

  • Likelihood of User-Item Latent Score:

    \[\begin{aligned} x_{i,j} \mid \overrightarrow{\mathbf{u}}_{i}, \overrightarrow{\mathbf{v}}_{j} &\sim \mathcal{N}\left(\langle\overrightarrow{\mathbf{u}}_{i}, \overrightarrow{\mathbf{v}}_{j}\rangle, \tau^{-1}\right) \end{aligned}\]

Part.2 Variational AutoEncoder

  • If Data Point \(\overrightarrow{\mathbf{x}}_{j}\) is generated by Parameter \(\overrightarrow{\mathbf{z}}_{j}\), Likelihood of \(\overrightarrow{\mathbf{x}}_{j}\):

    \[\overrightarrow{\mathbf{x}}_{j} \mid \overrightarrow{\mathbf{z}}_{j} \sim \mathcal{L}\left(\Theta \right)\]

  • Prior Determination of \(\overrightarrow{\mathbf{z}}_{j}\):

    \[\overrightarrow{\mathbf{z}}_{j} \sim \mathcal{N}\left(0, \mathbf{I}_{K}\right)\]

  • Posterior Estimation of \(\overrightarrow{\mathbf{z}}_{j}\):

    \[p\left(\overrightarrow{\mathbf{z}}_{j} \mid \overrightarrow{\mathbf{x}}_{j} ; \Theta\right) \propto \mathcal{L}\left(\overrightarrow{\mathbf{x}}_{j} \mid \overrightarrow{\mathbf{z}}_{j} ; \Theta \right) \cdot \pi\left(\overrightarrow{\mathbf{z}}_{j}\right)\]

  • \(\overrightarrow{\mathbf{z}} \sim Q(\Phi)\), Approximate Dist. of \(\overrightarrow{\mathbf{z}} \mid \overrightarrow{\mathbf{x}} \sim P(\Theta)\) Definition:

    \[\begin{aligned} q\left(\overrightarrow{\mathbf{z}}_{j} ; \Phi\right) &= \mathcal{N}\left(\mu(\overrightarrow{\mathbf{x}}_{j} ; \Phi), \text{diag}[\sigma^2(\overrightarrow{\mathbf{x}}_{j} ; \Phi)]\right)\\ &\approx \mu(\overrightarrow{\mathbf{x}}_{j} ; \Phi) + \sigma(\overrightarrow{\mathbf{x}}_{j} ; \Phi) \odot \epsilon \quad \text{for} \quad \epsilon \sim \mathcal{N}\left(0, \mathbf{I}_{K}\right) \end{aligned}\]

Optimization

  • Prediction

    \[\hat{r}_{i,j} = \langle\overrightarrow{\mathbf{u}}^{*}_{i}, \overrightarrow{\mathbf{v}}^{*}_{j} + \mathbb{E}\left[\overrightarrow{\mathbf{z}}^{*}_{j}\right]\rangle\]

  • Objective Function

    \[\mathcal{J} = \underbrace{\overbrace{\text{MSE}}^{-\text{Log Likelihood}} + \overbrace{\frac{\tau}{2} \left(\Vert \mathbf{U} \Vert^{2} + \Vert \mathbf{V} \Vert^{2}\right)}^{-\text{Log Priors}}}_{\text{Bayesian Matrix Factorization}} - \underbrace{\text{ELBO} + \lambda_{\Phi} \Vert \Phi \Vert^{2} + \lambda_{\Theta} \Vert \Theta \Vert^{2}}_{\text{Variational AutoEncoder}}\]

    • MSE 항

      \[\text{MSE} = \sum_{(i,j) \in \Omega}{\Vert r_{i,j} - \hat{r}_{i,j} \Vert^{2}}\]

    • ELBO 항

      \[\text{ELBO} = \underbrace{\mathbb{E}_{\mathbf{z} \sim Q(\Phi)}\left[\log{\mathcal{L}\left(\overrightarrow{\mathbf{x}}_{j} \mid \overrightarrow{\mathbf{z}}_{j};\Theta\right)}\right]}_{-\text{Reconstruction Loss}} - \underbrace{D_{KL}\left[q\left(\overrightarrow{\mathbf{z}}_{j} ; \Phi\right)\parallel \pi\left(\overrightarrow{\mathbf{z}}_{j}\right)\right]}_{\text{KL Divergence}}\]

  • Optimization

    \[\overrightarrow{\mathbf{u}}_{i}^{*}, \overrightarrow{\mathbf{v}}_{j}^{*}, \Phi^{*}, \Theta^{*} \mid K, \tau = \text{arg}\min{\mathcal{J}}\]
    • \(\overrightarrow{\mathbf{u}}_{i}^{*}\) : MAP of User-Latent Factor Vector, Params of Baeysian Matrix Factorization
    • \(\overrightarrow{\mathbf{v}}_{j}^{*}\) : MAP of Item-Latent Factor Vector, Params of Baeysian Matrix Factorization
Research Interest, Recommender System
Paper Review Data Mining Recommender System Collaborative Filtering Latent Factor Model Deep Learning Autoencoder Implicit Feedback Bayesian
This post is licensed under CC BY 4.0 by the author.