Mult-VAE

Mult-VAE

---

• 문제 의식
  • Implicit Feedback Problem
    • 구조적 편향 문제(Structural Bias): 관측을 선호, 미관측을 비선호로 확정적으로 간주하기에 불확실한 요소가 존재함(관측 불완전성)
    • 클래스 불균형 문제(Class Imbalance): 관측과 미관측의 비율이 균등하지 않아 모든 상호작용을 $0$ 으로 예측할 위험이 있음(데이터 희소성)

  • Competitive Relationship between Items: 사용자 선택 과정에는 아이템 간 암묵적인 경쟁적 구조가 존재하므로 사용자가 특정 아이템과 상호작용할 확률은 다른 아이템과 상호작용할 확률과 독립적으로 계산되어서는 안 됨

  • Uncertainty of Latent Representation: 관측 불완전성, 데이터 희소성 등 암시적 피드백 데이터의 정보 불확실성으로 인하여 사용자 잠재 선호를 확정적으로 도출하기에 문제가 있으므로 사용자 선호가 취할 수 있는 다양한 가능성을 고려해야 함
• Mult-VAE(Multinomial Variational AutoEncoder): 확률적 생성 과정을 통해 표현의 다양성을 확보하되, 사전 정보로 규제함으로써 과잉 표현을 규제하고 일반화를 도모하는 오토인코더 기반 협업필터링 모형
  • Liang, D., Krishnan, R. G., Hoffman, M. D., & Jebara, T.
    (2018, April).
    Variational autoencoders for collaborative filtering.
    In Proceedings of the 2018 world wide web conference (pp. 689-698).

Notation

---

• $u=1,2,\cdots,M$: user idx
• $i=1,2,\cdots,N$: item idx
• $\mathbf{Y} \in \mathbb{R}^{M \times N}$: user-item implicit feedback matrix
• $f(\cdot)$: encoder networks
• $g(\cdot)$: decoder networks

How to Modeling

---

• Bayesian Framework

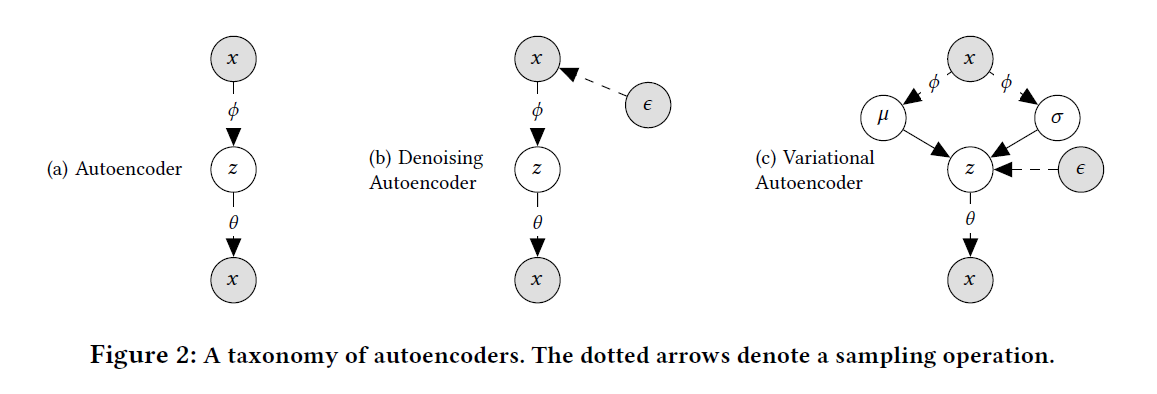
  • $Q$ is approx. dist. of latent preference vector:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u} \sim \mathcal{N}(\mu_{u}, \text{diag}(\sigma_{u}^{2})) \end{aligned}\]
    • $\mu_{u}, \text{diag}(\sigma_{u}^{2})$ is inferred by encoder networks $f(\cdot)$

  • $\Pi$ is prior dist. of latent preference vector:

    \[\begin{aligned} \overrightarrow{\mathbf{z}}_{u} \sim \mathcal{N}(0, \mathbf{I}) \end{aligned}\]

  • $P$ is likelihood:

    \[\begin{aligned} \overrightarrow{\mathbf{y}}_{u} \mid \overrightarrow{\mathbf{z}}_{u} \sim \text{Multinomial}(\vert \mathcal{R}_{u}^{+} \vert, \delta[g(\overrightarrow{\mathbf{z}}_{u})]) \end{aligned}\]
    • \(\overrightarrow{\mathbf{y}}_{u} \mid \overrightarrow{\mathbf{z}}_{u}\) is generated by decoder networks \(g(\cdot)\)
    • to reflect the competitive relationship between items when the user selects an item,
      • likelihood is multinomial dist., not $n$ independent binomial dist.
      • $\delta(\cdot)$ is softmax function, not sigmoid function

• Objective Function is ELBO:

  \[\begin{aligned} \hat{\Theta} &= \text{arg} \max{\mathbb{E}_{\mathbf{Z} \mid \mathbf{Y} \sim Q}[\log{p(\overrightarrow{\mathbf{y}}_{u} \mid \overrightarrow{\mathbf{z}}_{u})}] - \beta \cdot KL[Q(\overrightarrow{\mathbf{z}}_{u}) \Vert \Pi(\overrightarrow{\mathbf{z}}_{u})]} \end{aligned}\]