Variable Issues

Qualitative Predictors

---

Level 2

어느 신용카드 사에서 고객이 학생인지 여부에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 학생인 사람의 신용카드 대금 평균
  • $\beta_1$ : 학생인 사람과 학생이 아닌 사람의 신용카드 대금 평균 차이

Level 3

어느 신용카드 사에서 고객의 인종(황인/흑인/백인)에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• 지시 변수(Indicate Variable)

  \[d_{1}^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if Black}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\\ \quad d_{2}^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if White}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d_{1}^{(i)} + \beta_{2} \cdot d_{2}^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if Black}\\ \beta_{0} + \beta_{2} + \varepsilon^{(i)} \quad &\text{if White}\\ \beta_{0} + \varepsilon^{(i)} \quad &\text{if Asian} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 황인의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 흑인의 신용카드 대금 평균
  • $\beta_1$ : 황인과 흑인의 신용카드 대금 평균 차이
  • $\beta_0 + \beta_2$ : 백인의 신용카드 대금 평균
  • $\beta_2$ : 황인과 백인의 신용카드 대금 평균 차이

Qualitative & Quantitative

어느 신용카드 사에서 고객의 신용카드 대금에 관한 회귀 모형을 설계하고자 한다. 고객의 수입과 학생 여부에 관한 데이터를 확보하고 있다.

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 $x$(Income)이 동일한 수준일 때 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : $x$(Income)이 동일한 수준일 때 학생인 사람의 신용카드 대금 평균
  • $\beta_1$ : $x$(Income)이 동일한 수준일 때 학생인 사람과 학생이 아닌 사람의 신용카드 대금 평균 차이
  • $\beta_2$ : 학생 여부와 무관하게, $x$(Income) 단위 변동에 따른 $y$ 의 변동성

Effect Coding

어느 신용카드 사에서 고객이 학생인지 여부에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• Effect Coding : 각 범주의 효과를 비교하기 위하여 참조 수준을 명시적으로 사용하지 않고 전체 평균과 비교하는 범주형 변수 인코딩 방법

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ -1 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} - \beta_{1} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 모든 사람들의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 학생인 사람의 신용카드 대금 평균
  • $\beta_0 - \beta_1$ : 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_1$ : 학생 여부에 따른 신용카드 대금 평균의 차이

Interaction Terms

---

• 상호작용 효과 (Interaction Effect) : 두 개 이상의 설명변수가 결합하여 반응변수에 미치는 영향이, 각 설명변수의 주효과를 가산한 것과 다를 때 발생하는 효과로서, 한 설명변수가 반응변수에 미치는 효과가 다른 설명변수의 수준에 영향을 받는 경우 발생함

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot x_{1}^{(i)} + \beta_{2} \cdot x_{2}^{(i)} + \underbrace{\beta_{3} \cdot x_{1}^{(i)}x_{2}^{(i)}}_{\text{Interaction Term}} + \varepsilon^{(i)}\\ &= \beta_{0} + \underbrace{\left(\beta_{1} + \beta_{3} \cdot x_{2}^{(i)}\right)}_{\tilde{\beta}_{1}} \cdot x_{1}^{(i)} + \beta_{2} \cdot x_{2}^{(i)} + \varepsilon^{(i)}\\ &= \beta_{0} + \beta_{1} \cdot x_{1}^{(i)} + \underbrace{\left(\beta_{2} + \beta_{3} \cdot x_{1}^{(i)}\right)}_{\tilde{\beta}_{2}} \cdot x_{2}^{(i)} + \varepsilon^{(i)} \end{aligned}\]
  • 주효과(Main Effect; $\beta_{1}, \beta_{2}$) : 설명변수가 반응변수에 독립적으로 미치는 직접적인 효과
  • 시너지 효과(Synergy Effect; $\beta_{3}$) : 설명변수 간 상호작용을 통해 나타나는, 가산적이지 않은 효과

• 계층적 원리(Hierarchical Principle)

  교호작용 효과(Interaction Effect)의 유효성이 입증되어 모형에 포함하는 경우, 해당 교호작용을 구성하는 주효과(Main Effects)는 유효성 여부와 상관없이 모형에 포함해야 함. 주효과를 제외하는 경우 교호작용 효과 해석이 불분명해질 수 있기 때문임. 가령 실제 상호작용 효과가 아니라, 주효과의 부분적인 영향을 나타낼 수 있음.

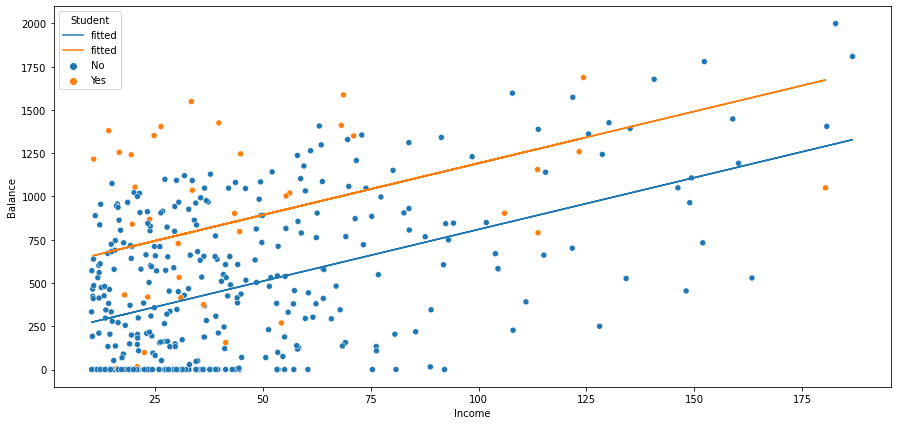
• 범주형 설명변수와 연속형 설명변수 간 교호작용 효과

  어느 신용카드 사에서 고객의 신용카드 대금에 관한 회귀 모형을 설계하고자 한다. 고객의 수입과 학생 여부에 관한 데이터를 확보하고 있다. 이때 수입과 학생 여부에 대한 교호작용 효과의 유효성을 알아보고자 한다.

  • 지시 변수(Indicate Variable)

    \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

  • 선형 회귀 모형

    학생 여부와 수입 간 교호작용 효과가 있다는 것보다는 학생일 때와 학생이 아닐 때 수입이 신용카드 대금에 미치는 영향력에 차이가 있다는 것으로 해석하는 것이 바람직함

    \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \beta_{2} \cdot x^{(i)} + \beta_{3} \cdot d^{(i)} x^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \left(\beta_{0} + \beta_{1}\right) + \left(\beta_{2} + \beta_{3}\right) \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
    • $\beta_2$ : 학생이 아닌 사람의 $x$(Income) 단위 변동에 따른 $y$ 변동성
    • $\beta_2 + \beta_3$ : 학생인 사람의 $x$(Income) 단위 변동에 따른 $y$ 변동성