Posterior Estimation (2) Information Theory

Information Theory

---

• 정보이론(Information Theory) : 신호에 존재하는 정보의 양을 측정하는 이론으로서, 특정 확률분포의 특성을 알아내거나, 두 확률분포 간 유사성을 정량화하는 데 사용함

Information Gain

• 자기정보(Self-Information) : 확률변수 $X \sim P$ 에 대하여, 사건 $X=x$ 가 발생했을 때의 정보량

  \[\begin{aligned} I(X=x) &= \log{\frac{1}{P(X=x)}}\\ &=-\log{P(X=x)} \end{aligned}\]
  • 자주 발생하지 않는 사건(Unlikely Event)일수록 높은 정보량을 가짐(Informative)
  • 독립사건은 추가적인 정보량을 가짐(Addictive Information)
    • 동전을 두 번 던져서 앞면이 두 번 나오는 사건은 동전을 한 번 던져서 앞면이 나오는 사건보다 정보량이 두 배임

• 엔트로피(Entropy) : 자기정보의 기대값으로서, 주어진 확률분포에서 발생 가능한 사건들의 평균적인 정보량

  \[\begin{aligned} H(P) &= \mathbb{E}_{X \sim P}\left[I(X)\right]\\ &= \mathbb{E}_{X \sim P}\left[-\log{P(X)}\right]\\ &= -\mathbb{E}_{X \sim P}\left[\log{P(X)}\right]\\ &= -\sum_{x}{\log{P(x)} \cdot P(x)} \end{aligned}\]
  • 사건의 분포가 결정적일수록(Deterministic) 엔트로피가 감소함
  • 사건의 분포가 균등할수록(Uniform) 엔트로피가 증가함

Information Discrepancy

• 교차 엔트로피(Cross Entropy) : 확률변수 $X$ 의 분포 $P$ 와 그 근사 분포 $Q$ 에 대하여, $Q$ 가 $P$ 에 대하여 제공하는 정보의 불확실성을 측정하는 지표

  \[\begin{aligned} H(P,Q) &= \mathbb{E}_{X \sim P}\left[-\log{Q(X)}\right]\\ &= - \sum_{x}{\log{Q(x)} \cdot P(x)} \end{aligned}\]

• 쿨백 라이블러 발산(Kullback-Leibler Divergence) : 확률변수 $X$ 의 분포 $P$ 와 그 근사 분포 $Q$ 에 대하여, $Q$ 를 $P$ 의 근사 분포로 사용할 때의 비효율성을 측정하는 지표로서, $P$ 에서 샘플링된 $X$ 에 대하여, $P$ 가 제공하는 평균적인 정보량과 $Q$ 가 제공하는 평균적인 정보량의 차이

  \[\begin{aligned} D_{KL}(P \parallel Q) &= \mathbb{E}_{X \sim P}\left[-\log{P(X)}\right] - \mathbb{E}_{X \sim P}\left[-\log{Q(X)}\right]\\ &= \mathbb{E}_{X \sim P}\left[-\log{\frac{Q(X)}{P(X)}}\right]\\ &= \mathbb{E}_{X \sim P}\left[\log{\frac{P(X)}{Q(X)}}\right]\\ &= \sum_{x}{\log{\frac{P(x)}{Q(x)}} \cdot P(x)} \end{aligned}\]

• 교차 엔트로피와 쿨백 라이블러 발산의 관계

  \[\begin{aligned} D_{KL}(P \parallel Q) &= \sum_{x}{\log{\frac{P(x)}{Q(x)}} \cdot P(x)}\\ &= -\sum_{x}{\log{\frac{Q(x)}{P(x)}} \cdot P(x)}\\ &= -\sum_{x}{\left[\log{Q(x)}-\log{P(x)}\right] \cdot P(x)}\\ &= \left[-\sum_{x}{\log{Q(x)} \cdot P(x)}\right] -\left[-\sum_{x}{\log{P(x)} \cdot P(x)}\right]\\ &= H(P,Q) - H(P) \end{aligned}\]

Bayes by Backprop

---

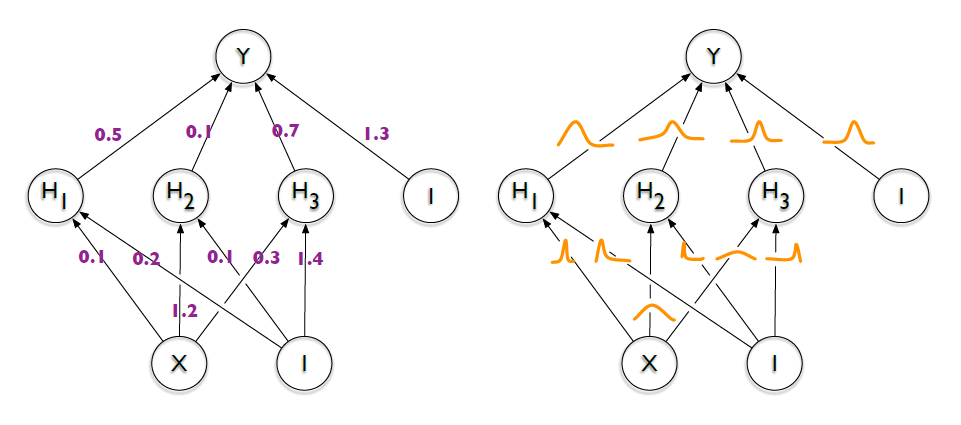
• BBB(Bayes by Backprop) : 신경망과 같은 복잡한 모형에서, 역전파 알고리즘을 활용한 최적화 학습을 통해 파라미터의 사후 분포를 추정하기 위해 정보 이론적 접근을 사용하는 베이지안 추론 방법론
  • 파라미터의 사후 확률 분포 추정 방법 : 변분 추론(Variational Inference)
  • 손실 함수 : 변분 자유 에너지(Variational Free Energy; VFE)
  • 역전파 트릭 : 재매개변수화 트릭(Reparameterization Trick)
  • 과적합 방지 트릭 : 후방 템퍼링(Posterior Tempering)
• 제안 논문 : Weight Uncertainty in Neural Networks, ICML, 2015

Variational Inference

• 변분 추론(Variational Inference) : 최적화 기법을 사용하여 가중치의 사후 분포 $W \mid \mathcal{D} \sim P$ 에 근사하는 제안 분포 $W \mid \theta \sim Q$ 를 탐색하는 방법

  \[\begin{aligned} \hat{\theta} &= \text{arg}\min_{\theta}{D_{KL}\big[Q(W \mid \theta) \parallel P(W \mid \mathcal{D})\big]} \end{aligned}\]

• 이상적인 접근 : 가중치 $W$ 에 대한 사후 분포 $W \mid \mathcal{D} \sim P$ 를 잘 설명하는 제안 분포 $W \mid \theta \sim Q$ 를 탐색함

  \[\begin{aligned} D_{KL}\big[P(W \mid \mathcal{D}) \parallel Q(W \mid \theta)\big] &= \mathbb{E}_{W \mid \mathcal{D} \sim P}\left[\log{\frac{P(W \mid \mathcal{D})}{Q(W \mid \theta)}}\right] \end{aligned}\]
  • 추론 대상이 되는 분포 $P$ 에서 $W$ 를 샘플링하는 것은 현실적으로 불가능함

• 대안 : 가중치 $W$ 에 대한 사후 분포 $W \mid \mathcal{D} \sim P$ 로 잘 설명될 수 있는 제안 분포 $W \mid \theta \sim Q$ 를 탐색함

  \[\begin{aligned} D_{KL}\big[Q(W \mid \theta) \parallel P(W \mid \mathcal{D})\big] &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{\frac{Q(W \mid \theta)}{P(W \mid \mathcal{D})}}\right] \end{aligned}\]
  • 즉, 제안분포 $Q$ 에서 $W$ 를 샘플링한 후, $W$ 에 대하여 $Q$ 와 $P$ 가 제공하는 정보량의 차이를 계산함

VFE

• 사후 분포 $W \mid \mathcal{D} \sim P$ 와 그 근사 분포 $W \mid \theta \sim Q$ 의 차이 세분화

  \[\begin{aligned} D_{KL}\big[Q(W \mid \theta) \parallel P(W \mid \mathcal{D})\big] &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{\frac{Q(W \mid \theta)}{P(W \mid \mathcal{D})}}\right]\\ &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{Q(W \mid \theta)}\right] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(W \mid \mathcal{D})}\right]\\ &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{Q(W \mid \theta)}\right] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{\frac{P(\mathcal{D} \mid W) \cdot P(W)}{P(\mathcal{D})}}\right]\\ &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{Q(W \mid \theta)}\right] - \bigg(\mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] + \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(W)}\right] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D})}\right]\bigg)\\ &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{Q(W \mid \theta)} - \log{P(W)}\right] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] + \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D})}\right]\\ &= D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] + \log{P(\mathcal{D})} \end{aligned}\]
  • $D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big]$ : 사후 분포의 근사 분포 $W \mid \theta \sim Q$ 와 사전 분포 $W \sim P$ 의 차이
  • $\mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right]$ : 사후 분포의 근사 분포 $W \mid \theta \sim Q$ 에서 샘플링된 가중치 $W$ 에 대한 로그 우도의 기대값
  • $\log{P(\mathcal{D})}$ : 데이터 $\mathcal{D}$ 에 대한 로그 마진 우도(Marginal Liklihood)로서, $\mathcal{D}$ 가 발생할 확률

• $\log{P(\mathcal{D})}$ 의 이해

  \[\begin{aligned} D_{KL}\big[Q(W \mid \theta) \parallel P(W \mid \mathcal{D})\big] &= D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big] - \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] + \log{P(\mathcal{D})}\\ \log{P(\mathcal{D})} &= D_{KL}\big[Q(W \mid \theta) \parallel P(W \mid \mathcal{D})\big] + \bigg(\mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] - D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big]\bigg)\\ \therefore \log{P(\mathcal{D})} &\ge \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] - D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big] \end{aligned}\]

• 증거 하한(Evidence Lower B ound; ELBO) : 파라미터 갱신 증거 $\log{P(\mathcal{D})}$ 의 하한값

  \[\begin{aligned} \text{ELBO} &= \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] - D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big] \end{aligned}\]

  • 왜 $\log{P(\mathcal{D})}$ 가 파라미터 갱신 증거(Evidence)인가?

    데이터 발생 원리는 모수에 있음.
    다만, 빈도주의 철학에서 이는 절대적인 진리인데 반해, 베이지안 철학에서는 불확실한 값임. 따라서 베이지안 방법론에서는 모수를 확률변수로 설정하여 모델링함. 구체적으로는 모수에 대한 연구자의 사전 신념(Prior)을 바탕으로 증거를 관측하며 이 신념을 갱신해 감(Posterior).
    실현된 데이터는 모수, 즉 데이터 발생 원리에 대하여 가지고 있었던 초기 신념(Prior)을 뒷받침하거나 갱신하는(Posterior) 근거로서 활용됨. 따라서 데이터 $\mathcal{D}$ 가 발생할 확률 $P(\mathcal{D})$ 은 갱신된 파라미터에 대한 증거(Evidence)임.

• 변분 자유 에너지(Variational Free Energy; VFE) : 증거 하한의 손실 함수화

  \[\begin{aligned} \text{VFE} &= -\text{ELBO}\\ \therefore \hat{\theta} &= \text{arg}\min_{\theta}{\text{VFE}} \end{aligned}\]

Reparameterization Trick

• 재매개변수화 트릭(Reparameterization Trick) : 역전파 알고리즘을 활용한 최적화 학습이 가능하도록 샘플링을 미분 가능한 함수로 변형하는 방법

  \[w \mid \theta \sim Q \quad \rightarrow \quad w = g(\epsilon, \theta)\]

  • 가중치 $w$ 가 정규 분포 $N(\mu,\sigma^2)$ 를 따르는 경우의 예시

    \[w \mid \mu,\sigma \sim N \quad \rightarrow \quad w = \mu + \sigma \cdot \epsilon\]

Posterior Tempering

• 후방 템퍼링(Posterior Tempering) : 데이터에 과적합되는 것을 방지하도록 우도 항목의 영향력을 할인하는 방법

  \[\begin{aligned} P(\theta \mid \mathcal{D}) &\approx \left[P(\mathcal{D} \mid \theta)\right]^{1/T} \cdot P(\theta) \end{aligned}\]

  • 변분 자유 에너지에 후방 템퍼링을 적용하는 경우의 예시

    \[\begin{aligned} \text{VFE} &= D_{KL}\big[Q(W \mid \theta) \parallel P(W)\big] - \frac{1}{T} \cdot \mathbb{E}_{W \mid \theta \sim Q}\left[\log{P(\mathcal{D} \mid W)}\right] \end{aligned}\]