Vector

Vector

---

• 벡터(Vector): 벡터 공간의 원소로서 크기와 원점으로부터 뱡향을 가지는 물리량

  \[\begin{aligned} \mathbf{x} &=\begin{bmatrix} x_{1}\\ x_{2}\\ \vdots\\ x_{N} \end{bmatrix} \end{aligned}\]

  • 원소(Element): 벡터를 구성하는 요소

    \[\begin{aligned} x_{1},x_{2},\cdots,x_{N} \end{aligned}\]

  • 차원(Dimension): 원소의 갯수

    \[\begin{aligned} \mathbf{x} \in \mathbb{R}^{N} \end{aligned}\]

• 특수한 벡터

  • 영벡터(Zero Vector): 벡터 공간에서의 덧셈에 대한 항등원이 되는 벡터

    \[\begin{aligned} \mathbf{0} &=\begin{bmatrix} 0\\ 0\\ \vdots\\ 0 \end{bmatrix} \end{aligned}\]

  • 단위 벡터(Unit Vector): 길이가 $1$ 인 벡터로서 정규 벡터(Normal Vector)라고도 함

    \[\begin{gathered} (\mathbf{e}_{i})_{j} =\begin{cases} 1,\quad \text{if} \ j=i\\ 0,\quad \text{if} \ j \ne i \end{cases}\\ \\ \mathbf{e}_{1} =\begin{bmatrix} 1\\ 0\\ 0\\ \vdots\\ 0 \end{bmatrix}, \mathbf{e}_{2} =\begin{bmatrix} 0\\ 1\\ 0\\ \vdots\\ 0 \end{bmatrix}, \mathbf{e}_{3} =\begin{bmatrix} 0\\ 0\\ 1\\ \vdots\\ 0 \end{bmatrix} \end{gathered}\]

Norm

---

• 유클리디안 노름(L-2 Norm): 벡터의 규모(Magnitude) 혹은 원점 $\mathbf{0}$ 으로부터의 길이(Length)를 측정하는 연산자

  \[\begin{aligned} \Vert \mathbf{x} \Vert &=\sqrt{\mathbf{x}^T\mathbf{x}} \end{aligned}\]
  • $\Vert \mathbf{x} \Vert \ge 0$
  • $\Vert \mathbf{x} \Vert = 0 \Rightarrow \mathbf{x} = \mathbf{0}$
  • $\Vert \beta \cdot \mathbf{x} \Vert =\vert \beta \vert \cdot \Vert \mathbf{x} \Vert$
  • $\Vert\mathbf{x}+\mathbf{y}\Vert \le \Vert\mathbf{x}\Vert+\Vert\mathbf{y}\Vert$

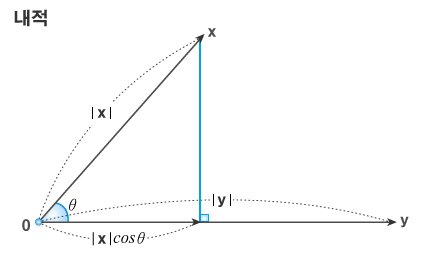
• 내적(Inner Product): 두 벡터 사이의 유사성 또는 정렬 정도를 측정하는 연산자로서, 그 결과값은 두 벡터가 원점을 기준으로 얼마나 같은 방향을 향하고 있는지를 나타냄

  \[\begin{aligned} \left<\mathbf{x},\mathbf{y}\right> &=\mathbf{x}^{T}\mathbf{y} \end{aligned}\]

• 코사인 유사도(Cosine Similarity): 두 벡터의 사이각 $\theta$ 의 코사인 값을 이용하여 측정한 벡터 간 유사도

  \[\begin{aligned} \cos{\theta}=\frac{\left<\mathbf{x},\mathbf{y}\right>}{\Vert\mathbf{x}\Vert\cdot\Vert\mathbf{y}\Vert} \end{aligned}\]
  • $-1\le \cos{\theta} \le 1$
  • $\cos{\theta} = -1$: 음의 유사도를 가진다고 볼 수 있으며 기하학적으로 상반된 방향성을 가짐
  • $\cos{\theta} = 1$: 양의 유사도를 가진다고 볼 수 있으며 기하학적으로 동일한 방향성을 가짐
  • $\cos{\theta} = 0$: 유사하다고 볼 수 없으며 기하학적으로 직교함

• 직교 정규 벡터(Orthonomal Vector): 임의의 벡터에 대하여 해당 벡터와 직교하는 정규 벡터

  

  • 정규 벡터(Normal Vector): 노름이 $1$ 인 벡터로서 단위 벡터

    \[\begin{aligned} \Vert \mathbf{x} \Vert &= 1 \end{aligned}\]

  • 상호 직교(Mutually Orthonal): 두 벡터가 서로 수직 관계에 있어 내적값이 $0$ 이 됨

    \[\begin{aligned} \mathbf{x} \perp \mathbf{y} \Leftrightarrow \frac{\left<\mathbf{x},\mathbf{y}\right>}{\Vert \mathbf{x} \Vert \cdot \Vert \mathbf{y} \Vert} = \cos{90^{\circ}} \end{aligned}\]

Linear Combination

---

• 스칼라-벡터 곱셈: 벡터의 모든 원소에 대한 스칼라 곱으로서, 벡터의 노름을 스칼라 비율로 확대 혹은 축소하는 연산으로 해석 가능함

  \[\begin{aligned} \alpha \times \mathbf{x} &=\begin{bmatrix} \alpha \times x_{1}\\ \alpha \times x_{2}\\ \vdots\\ \alpha \times x_{N} \end{bmatrix} \end{aligned}\]

• 덧셈과 뺄셈: 동차원 원소 간 합 혹은 차로서, 벡터 $\mathbf{x}$ 를 방향 $\mathbf{y}$ 으로 폭 $\Vert \mathbf{y} \Vert$ 만큼 평행이동하는 연산으로 해석 가능함

  \[\begin{aligned} \begin{bmatrix} x_{1}\\ x_{2}\\ \vdots\\ x_{N} \end{bmatrix} + \begin{bmatrix} y_{1}\\ y_{2}\\ \vdots\\ y_{N} \end{bmatrix} = \begin{bmatrix} x_{1}+y_{1}\\ x_{2}+y_{2}\\ \vdots\\ x_{N}+y_{N} \end{bmatrix} \end{aligned}\]

• 선형 결합(Linear Combination): 차원이 $n$ 으로 동일한 임의의 벡터와 스칼라에 대하여, 각 항에 스칼라를 곱하거나 상호 더함으로써 일련의 항으로 구성하는 작업

  \[\begin{aligned} \beta_{1}\mathbf{x}_{1} + \beta_{2}\mathbf{x}_{2} + \cdots + \beta_{p}\mathbf{x}_{p} \end{aligned}\]

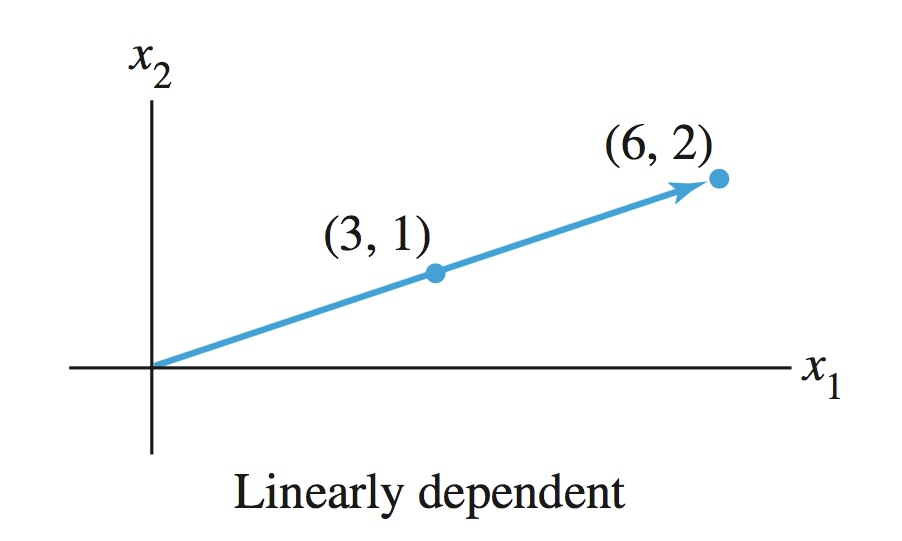
• 선형 종속(Linearly Dependent) : 어떤 벡터가 다른 벡터들의 선형 결합으로 표현 가능한 경우

  

  \[\begin{aligned} \beta_{1}\mathbf{x}_{1} + \beta_{2}\mathbf{x}_{2} + \cdots + \beta_{p}\mathbf{x}_{p} &=0, \quad \forall \beta \ne 0 \end{aligned}\]

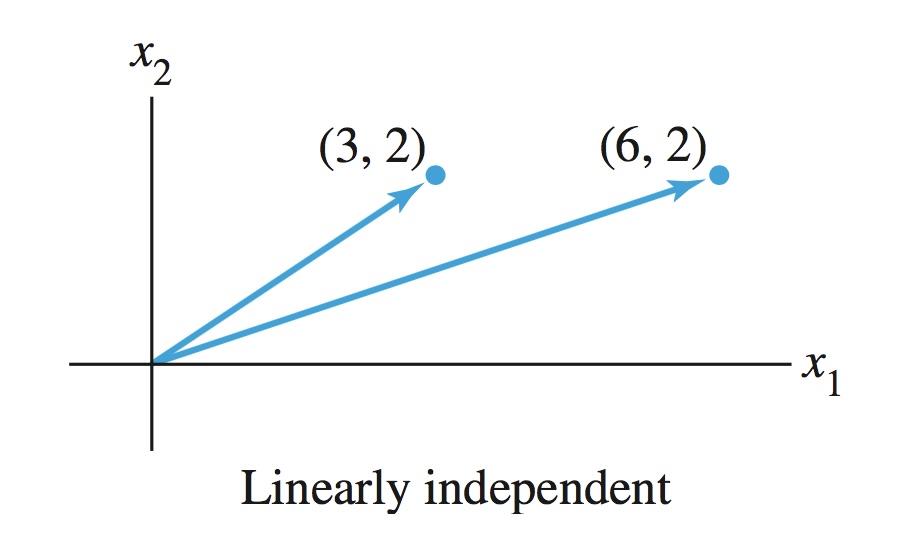
• 선형 독립(Linearly Independent) : 어떤 벡터가 다른 벡터들의 선형 결합으로 표현될 수 없는 경우

  

  \[\begin{aligned} \beta_{1}\mathbf{x}_{1} + \beta_{2}\mathbf{x}_{2} + \cdots + \beta_{p}\mathbf{x}_{p} &\ne 0, \quad \forall \beta \ne 0 \end{aligned}\]

• \(\mathrm{span}\): 벡터 공간 \(V\) 에서 선형 독립인 벡터들의 집합 \(S=\{\mathbf{v}_{1},\mathbf{v}_{2},\cdots,\mathbf{v}_{k}\}\) 이 주어졌을 때, 모든 가능한 선형 결합의 집합으로서, \(\forall \mathbf{v} \in S\) 가 생성 가능한 선형 공간, 혹은 이를 반환하는 생성자

  \[\begin{aligned} \mathrm{span}(S) &= \left\{\sum_{i=1}^{k}{\alpha_{i}\mathbf{v}_{i}} \mid \alpha_{i} \in \mathbb{F}\right\} \end{aligned}\]

• 기저(Basis): 부분 벡터 공간을 생성하는 직교 정규 벡터들의 집합으로서, $n$ 차원 벡터 공간을 총 $n$ 개의 직교 정규 벡터들을 $\mathrm{span}$ 하여 생성되며, 이때 기저들은 해당 벡터 공간의 축(axis)이 됨

  \[\begin{aligned} \begin{bmatrix} 3\\ 2 \end{bmatrix} &= 3 \times \mathbf{e}_{1} + 2 \times \mathbf{e}_{2} \end{aligned}\]