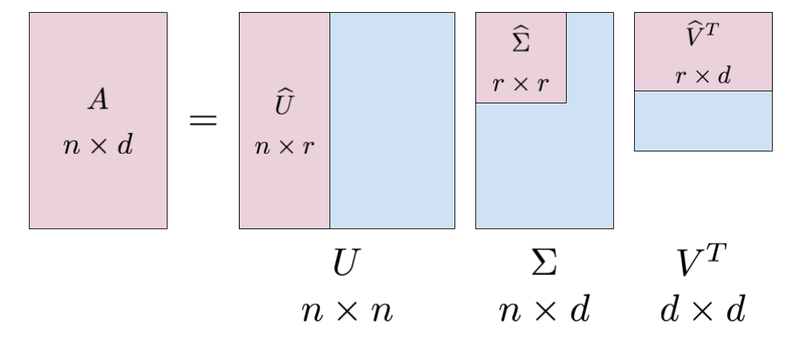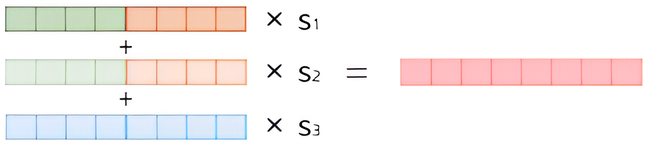WORD2VEC Improvements

Fast-Text

---

• Fast-Text : 내부 단어(Sub-word)를 고려한 임베딩 학습 방법론

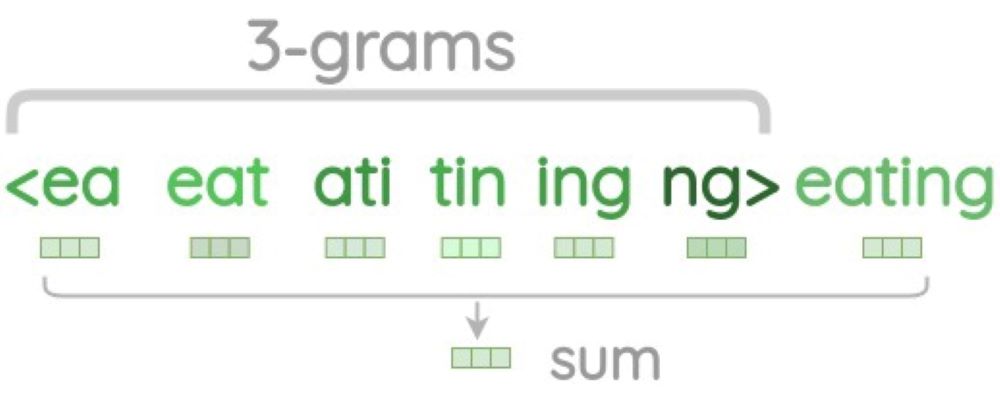
  EAT vs. EATING

  • WORD2VEC 의 한계점 : 단어의 형태학적 특성을 고려하지 않으므로, 비슷한 문맥에서 사용되지 않았다면 동일한 어근에서 파생된 단어들의 의미상 유사도를 반영할 수 없음
  • Fast-Text 의 해법 : 단어를 철자(Character) 단위의 n-gram 으로 간주하고, 단어 자체가 아니라 내부 단어들의 임베딩을 학습함
    • 통상 $3 \le n \le 6$ 으로 설정함

• EXAMPLE “eating”

  

  • Character $n$-grams of eating

    word	$n$	n-grams(sub-word)
    eating	3-gram	<ea, eat, ati, tin, ing, ng>
    eating	4-gram	<eat, eati, atin, ting, ing>
    eating	5-gram	<eati, eatin, ating, ting>
    eating	6-gram	<eatin, eating, ating>
    eating	Full	eating

  • Embedding Vector of eating

    \[\begin{aligned} \overrightarrow{\mathbf{z}} &= \text{Embedding}\left(\text{eating}\right) + \sum_{n}{\text{Embedding}\left(n\text{-grams}\right)} \end{aligned}\]

GloVe

---

• WORD2VEC, Fast-Text 의 한계점 : 말뭉치 내 Global Context 를 활용하지 못함

Co-occurrence Matrix based Method

• Co-occurrence Matrix : 말뭉치에서 각 단어가 윈도우 내에 다른 단어와 함께 등장하는 횟수를 측정한 행렬

  Counts	I	like	enjoy	deep	learning	NLP	flying	.
  I	0
  like		0
  enjoy			0
  deep				0
  learning					0
  NLP						0
  flying							0
  .								0

  • $X_{i,j} \in \mathbf{X}_{N \times N}$ : $i$ 번째 단어를 중심으로 했을 때 윈도우 내에 $j$ 번째 단어가 등장한 횟수

• PMI(Point Mutual Information) : 단순 횟수 측정 시 발생하는 고빈도 단어에 대한 잘못된 표현을 정정하기 위하여 고안된 측정 지표로서, 단어 $x$ 와 $y$ 가 동시에 발생할 확률을, 각각이 발생할 확률로 나눈 값

  \[\begin{aligned} PMI(A,B) &= \log{\frac{P(A,B)}{P(A)P(B)}}\\ &= \log{N} + \log{\text{Count}(A,B)} - \log{\text{Count}(A)} - \log{\text{Count}(B)} \end{aligned}\]

• PPMI(Positive Point Mutual Information) : 두 단어의 동시 발생 횟수가 $0$ 일 때 발생하는 음의 무한대로의 발산 문제를 해결한 측정 지표

  \[\begin{aligned} PPMI(A,B) &=\max\left(0, PMI(A,B)\right) \end{aligned}\]

• SVD 를 활용하여 고차원 문제 보완

  

  \[\begin{aligned} \mathbf{X}_{N \times N} \approx \underbrace{\mathbf{U}_{N \times N} \cdot \Sigma_{N \times D}}_{\text{Vector Representation}} \cdot \mathbf{V}^{T}_{N \times D} \end{aligned}\]

GloVe

• Co-occurrence Matrix based Method 의 한계점
  • 단어 간 유사도가 반영된 벡터 표현을 도출하지 못함
  • 고차원 행렬이기 때문에 SVD 등 차원 축소 기법을 추가로 활용해야 함

• GloVe(Global Vectors for Word Representation) : 단어 간 전역적 통계 정보를 활용하여 단어를 임베딩하는 방법론

  

  • 중심 단어 $i$ 와 주변 단어 $j$ 간 임베딩 벡터의 내적값이 동시 발생 확률이 되도록 학습함

    \[\begin{aligned} \overrightarrow{\mathbf{w}}_{i} \cdot \overrightarrow{\mathbf{v}}_{j} \approx \log{P(w_{j} \mid w_{i})} = \log{\frac{X_{i,j}}{\sum_{k}{X_{i,k}}}} \end{aligned}\]
    • $\overrightarrow{\mathbf{w}}_{i} \in \mathbf{W}$ : 단어 $i$ 가 중심 단어일 때의 임베딩 벡터
    • $\overrightarrow{\mathbf{v}}_{j} \in \mathbf{V}$ : 단어 $j$ 가 주변 단어일 때의 임베딩 벡터
    • $P(w_{j} \mid w_{i})$ : 중심 단어 $i$ 발생 조건부 $j$ 발생 확률
    • $\log{P(w_{j} \mid w_{i})}$ : 스케일 조정을 위하여 공동 발생 확률 자체가 아니라 공동 발생 확률의 로그값에 수렴하도록 학습함

  • 동시 발생 확률 $P(w_{j} \mid w_{i})$ 대신 동시 발생 횟수 $X_{i,j}$ 를 활용함

    \[\begin{aligned} \overrightarrow{\mathbf{w}}_{i} \cdot \overrightarrow{\mathbf{v}}_{j} \approx \log{X_{i,j}} \end{aligned}\]
    • 내적 값과 확률 값의 직접 대응이 어렵기 때문임($\because \sum_{j}{P(w_{j} \mid w_{i})}=1$)

• Loss Function

  \[\begin{aligned} \mathcal{L} &= \sum_{i,j}{f(X_{i,j})\left(\overrightarrow{\mathbf{w}}_{i} \cdot \overrightarrow{\mathbf{v}}_{j} + (b_{i} + \beta_{j}) - \log{X_{i,j}}\right)^{2}} \end{aligned}\]
  • \(f(X_{i,j})=\min{\left[1, \left(\displaystyle\frac{X_{i,j}}{X_{\text{max}}}\right)^{3/4}\right]}\) : 학습 중 고빈도 단어 영향력 조정 함수

ELMo

---

• FFNN 에 기반한 기존 방법론의 한계점 : 문장 전체의 문맥을 반영하지 못하여 동의어, 다형어에 대한 표현이 제대로 이루어지지 못함

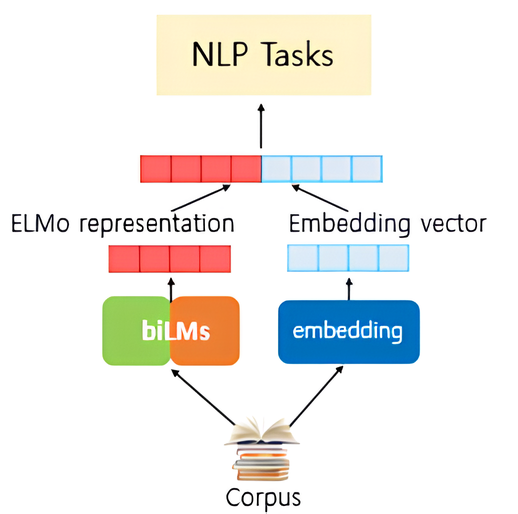
• ELMo(Embeddings from Language Model) : 방대한 텍스트 데이터로 사전 훈련된 LSTM 기반 언어 모형 BiLM 을 활용하는 단어 임베딩 방법론

  

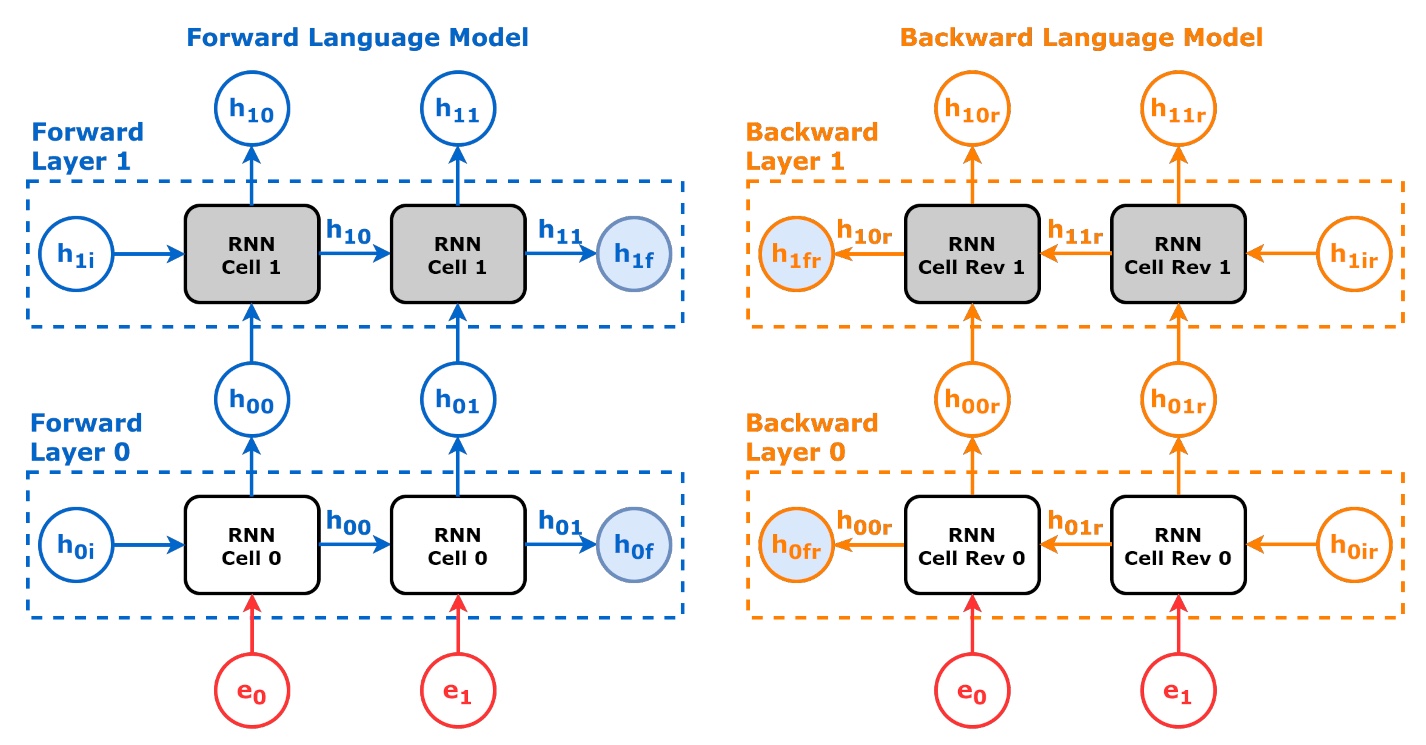
• BiLM(Bidirectional Language Model) : 문장 시퀀스를 순방향, 역방향으로 각각 학습하는 LSTM 기반 언어 모형

  

• Forward Path

  

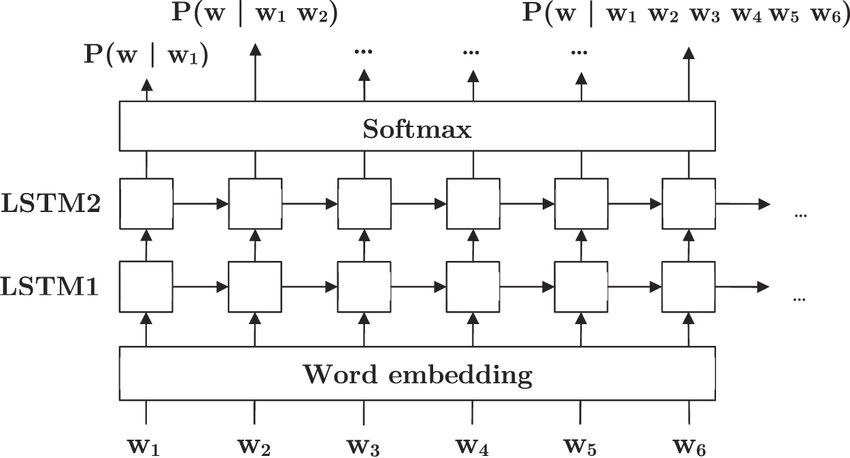
  1. Multi-Layer LSTM

     \[\begin{aligned} h^{(k)}_{t}, c^{(k)}_{t} &= \text{LSTM}^{(k)}\left(h^{(k-1)}_{t}, h^{(k)}_{t-1}, c^{(k)}_{t-1}\right) \end{aligned}\]
     • $h^{(k)}_{t}$ : $k$ 번째 LSTM Layer 의 $t$ 시점 은닉 값
       • 첫 번째 LSTM Layer 의 $t$ 시점 입력값 \(h^{(0)}_{t}\) 은 $t$ 시점 단어 $w_{t}$ 의 임베딩 벡터임
     • $c^{(k)}_{t}$ : $k$ 번째 LSTM Layer 의 $t$ 시점 셀 상태 값

  2. Output Layer

     \[\begin{aligned} \hat{\mathbf{y}} &= \text{F}_{\text{Softmax}}\left[h^{(K)}_{T}\right] \end{aligned}\]

• ELMo Representation

  

  \[\begin{aligned} \overrightarrow{\mathbf{w}}_{t} &= \sum_{k}{\gamma^{(k)}\left(h^{(k)}_{t} \oplus \eta^{(k)}_{t}\right)} \end{aligned}\]

---

Reference

• https://intoli.com/blog/pca-and-svd/
• https://github.com/dvgodoy/dl-visuals/
• https://www.researchgate.net/figure/The-recurrent-LSTM-language-model-structure-used-in-our-experiments_fig1_336086782
• https://wikidocs.net/33930