k-Means

k-Means

---

• k-Means: 중심점 기반 배타적 분리형 군집화 알고리즘으로서, 관측치와 중심점(Centroid) 간 평균 거리(Means)를 최소화하는 군집을 탐색함

  

  \[\begin{aligned} \min_{\mu_{i}}{\sum_{i=1}^{k}\sum_{\mathbf{x}_{j} \in C_{i}}{\Vert\mathbf{x}_{j}-\mu_{i}\Vert^{2}}} \end{aligned}\]

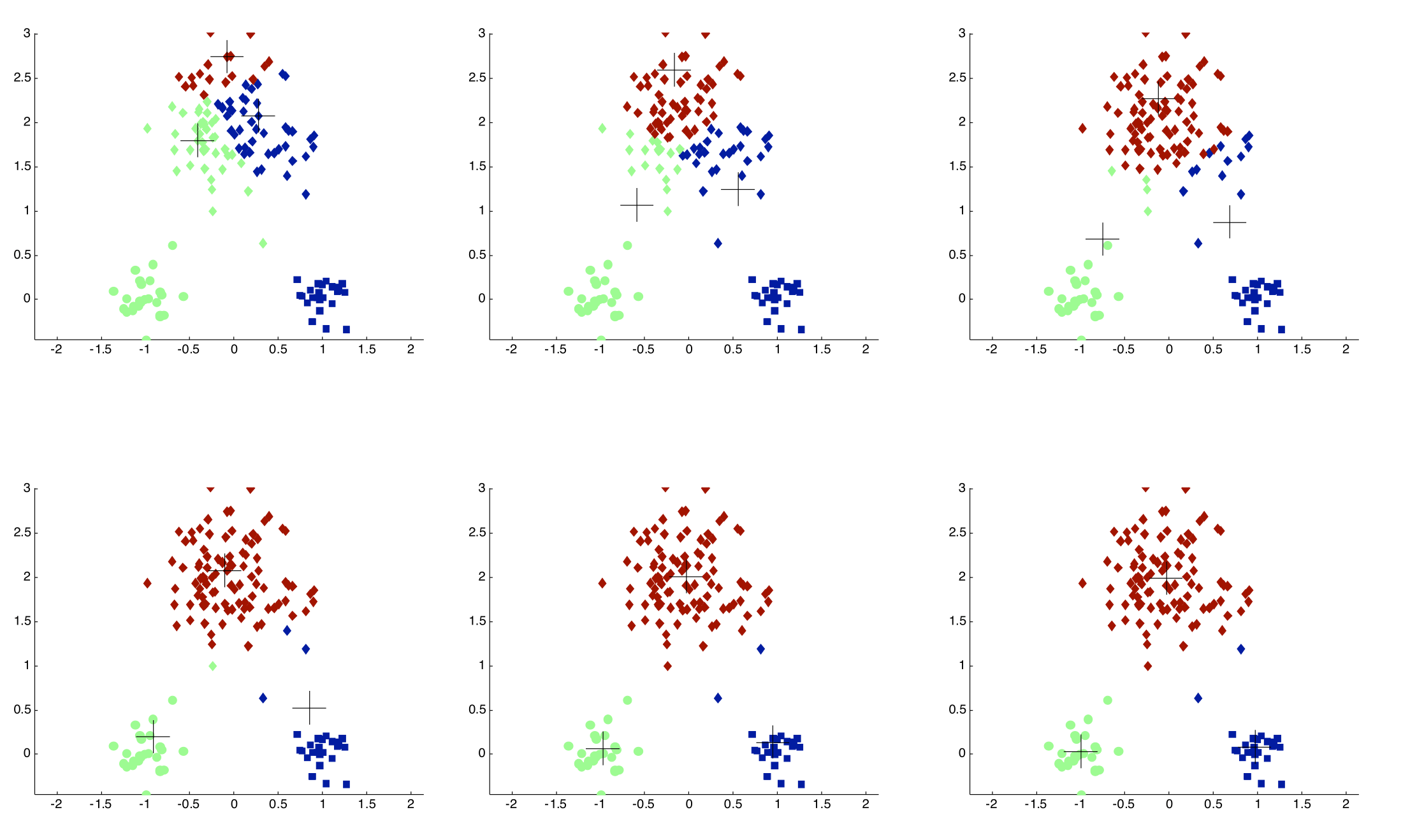
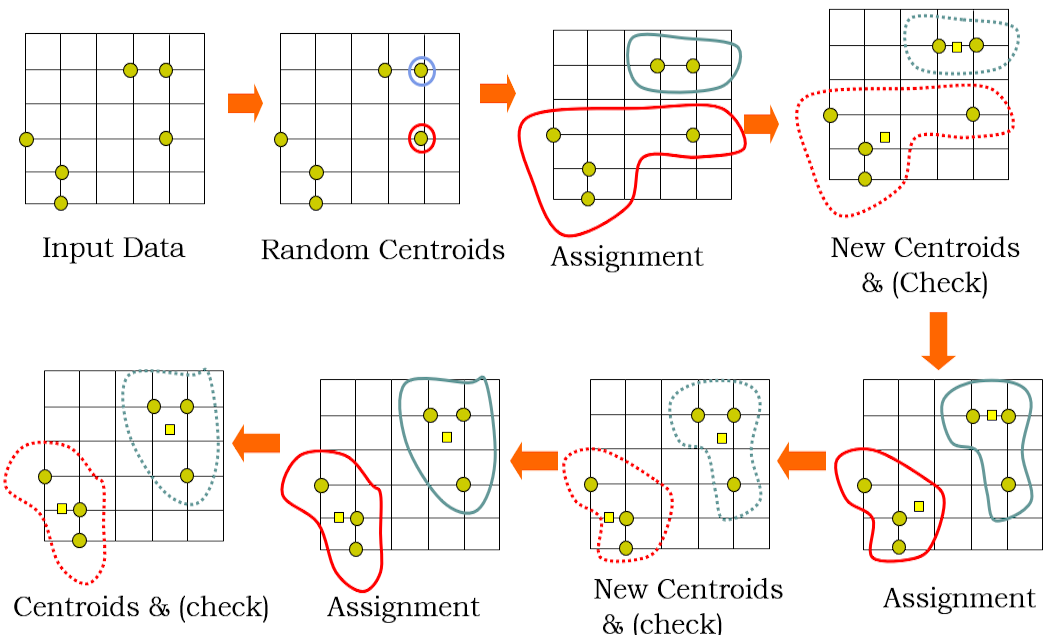
Centroid Search Process

---

1. 군집 갯수 설정

   \[\begin{aligned} X=C_{1} \cup C_{2} \cup \cdots \cup C_{k}, \quad C_{i} \cap C_{j \ne i} = \emptyset \end{aligned}\]

2. $k$ 개의 초기 군집 중심 벡터 $\mathbf{c}$ 임의 선정

   \[\begin{aligned} M=\left\{\mu_{1},\mu_{2},\cdots,\mu_{k}\right\} \end{aligned}\]

3. 모든 관측치 벡터 $\mathbf{x}$ 를 가장 가까운 거리에 위치한 중심 벡터 $\mu$ 의 군집에 배타적으로 할당

   \[\begin{aligned} \mathbf{x}_{j} \rightarrow C_{i} \quad \text{s.t.} \quad & i=\text{arg} \min_{i}{\Vert\mathbf{x}_{j}-\mu_{i}\Vert^{2}}\\ & \mu_{i} \in C_{i} \end{aligned}\]

4. 각 군집별 할당된 관측치 벡터들의 평균 벡터로 군집 중심 벡터 갱신

   \[\begin{aligned} \mu_{i} &=\frac{1}{\vert C_{i} \vert}\sum_{\mathbf{x}_{j}\in C_{i}}{\mathbf{x}_{j}} \end{aligned}\]

5. ③, ④의 과정을 반복하여 최적의 군집 중심 벡터 집합 $\hat{M}$ 탐색

   \[\begin{aligned} \hat{M} &= \left\{\mu_{i} \mid \text{arg} \min_{\mu_{i}}{\sum_{i=1}^{k}\sum_{\mathbf{x}_{j} \in C_{i}}{\Vert\mathbf{x}_{j}-\mu_{i}\Vert^{2}}}\right\} \end{aligned}\]

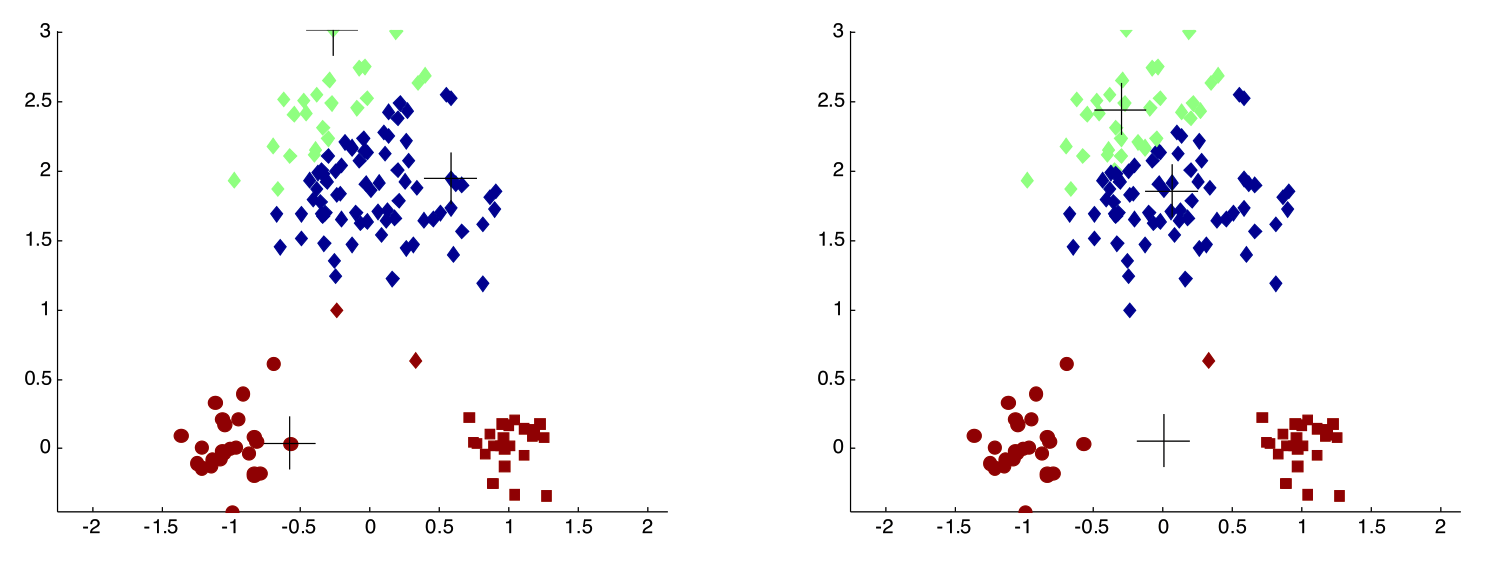
Limitation

---

• Sensitive to initial cluster centroids

  

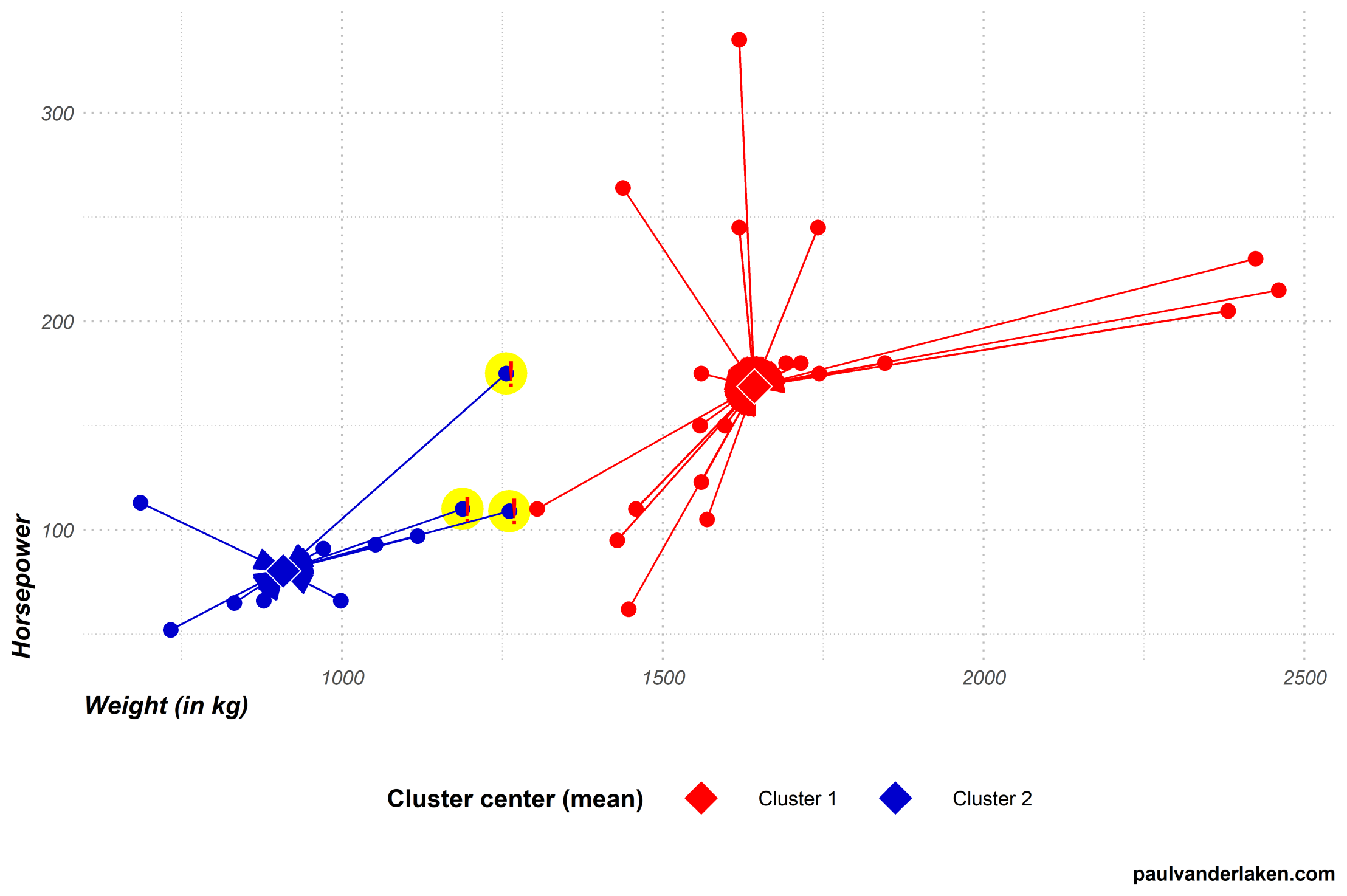
• Sensitive to outliers

  

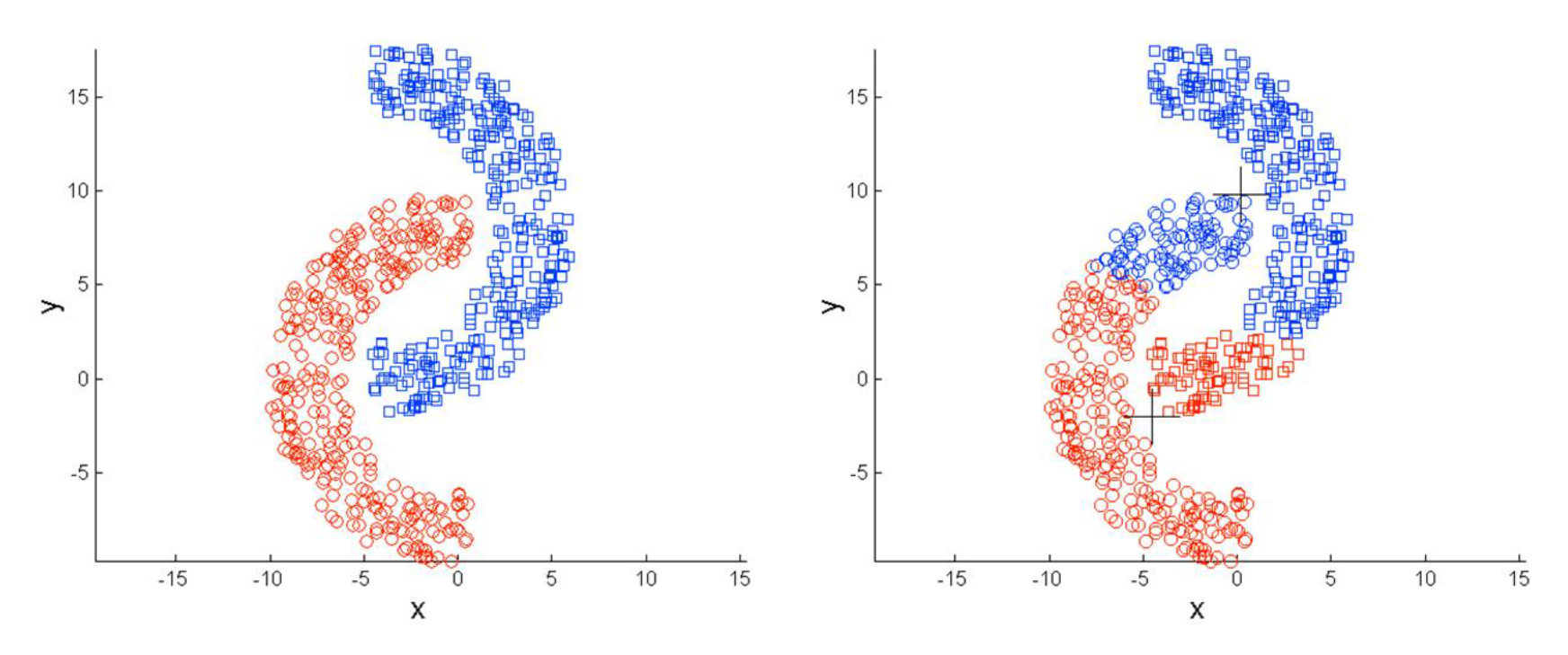
• Difficulty detecting clusters of non-spherical shapes

  

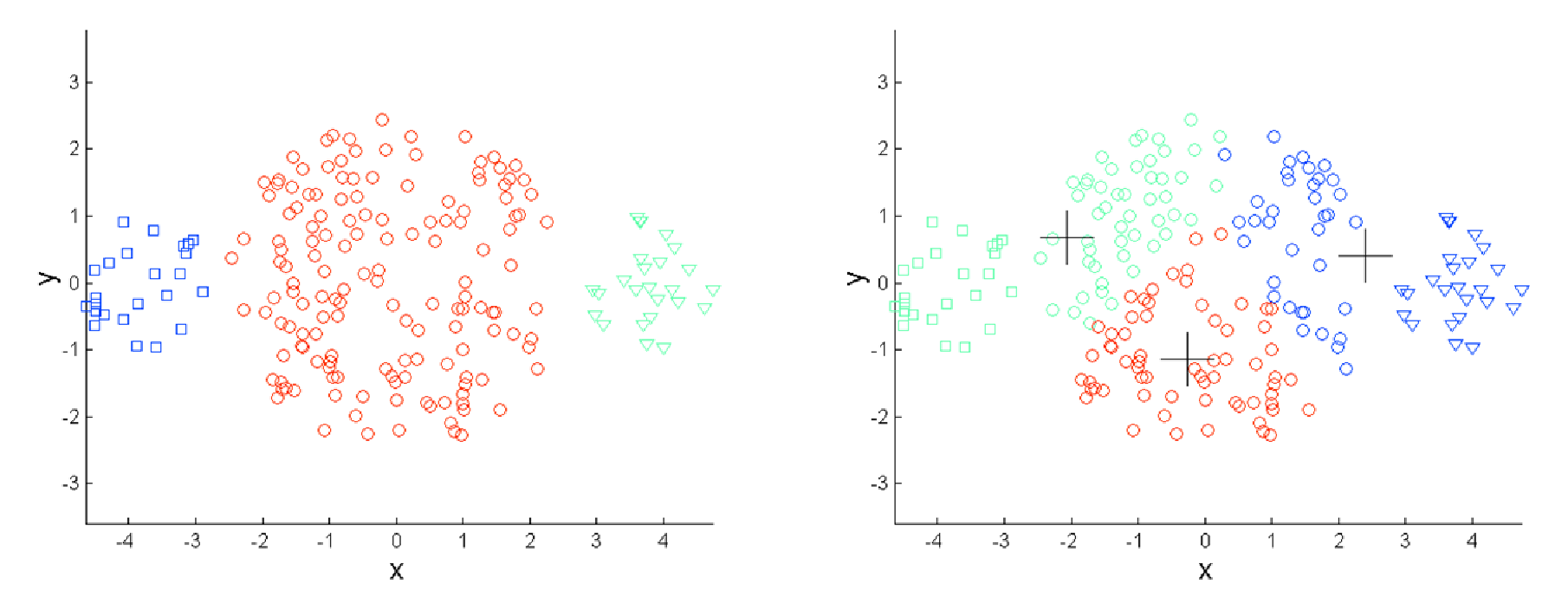
• Difficulty detecting clusters of different sizes

  

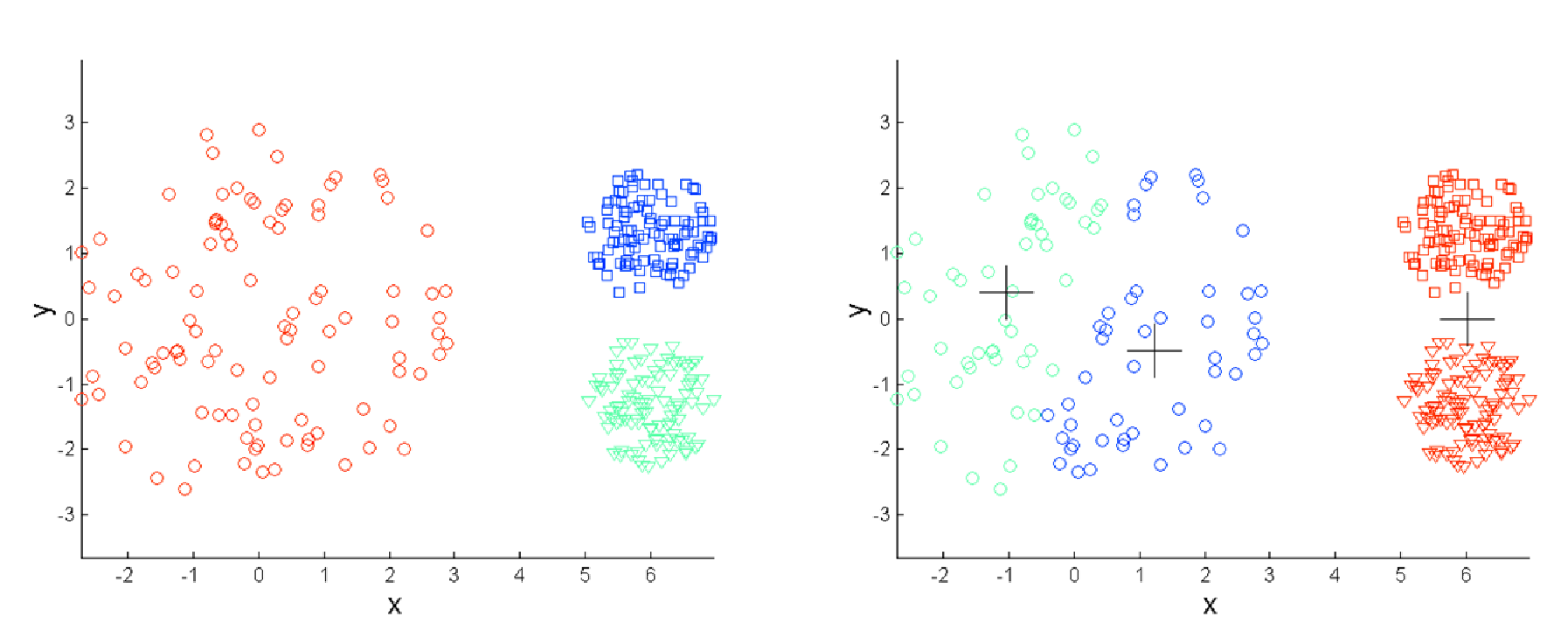
• Difficulty detecting clusters of different densities

  

---

Sourse

• https://ai-times.tistory.com/158
• https://github.com/pilsung-kang/multivariate-data-analysis/blob/master/09%20Clustering/09-2_K-Means%20Clustering.pdf
• https://github.com/lovit/python_ml_intro/blob/master/lecture_notes/10_clustering.pdf
• https://paulvanderlaken.com/2018/12/12/visualizing-the-inner-workings-of-the-k-means-clustering-algorithm/