k-NN
Based on the lecture “Intro. to Machine Learning (2023-2)” by Prof. Je Hyuk Lee, Dept. of Data Science, The Grad. School, Kookmin Univ.
k-Nearest Neighbors
-
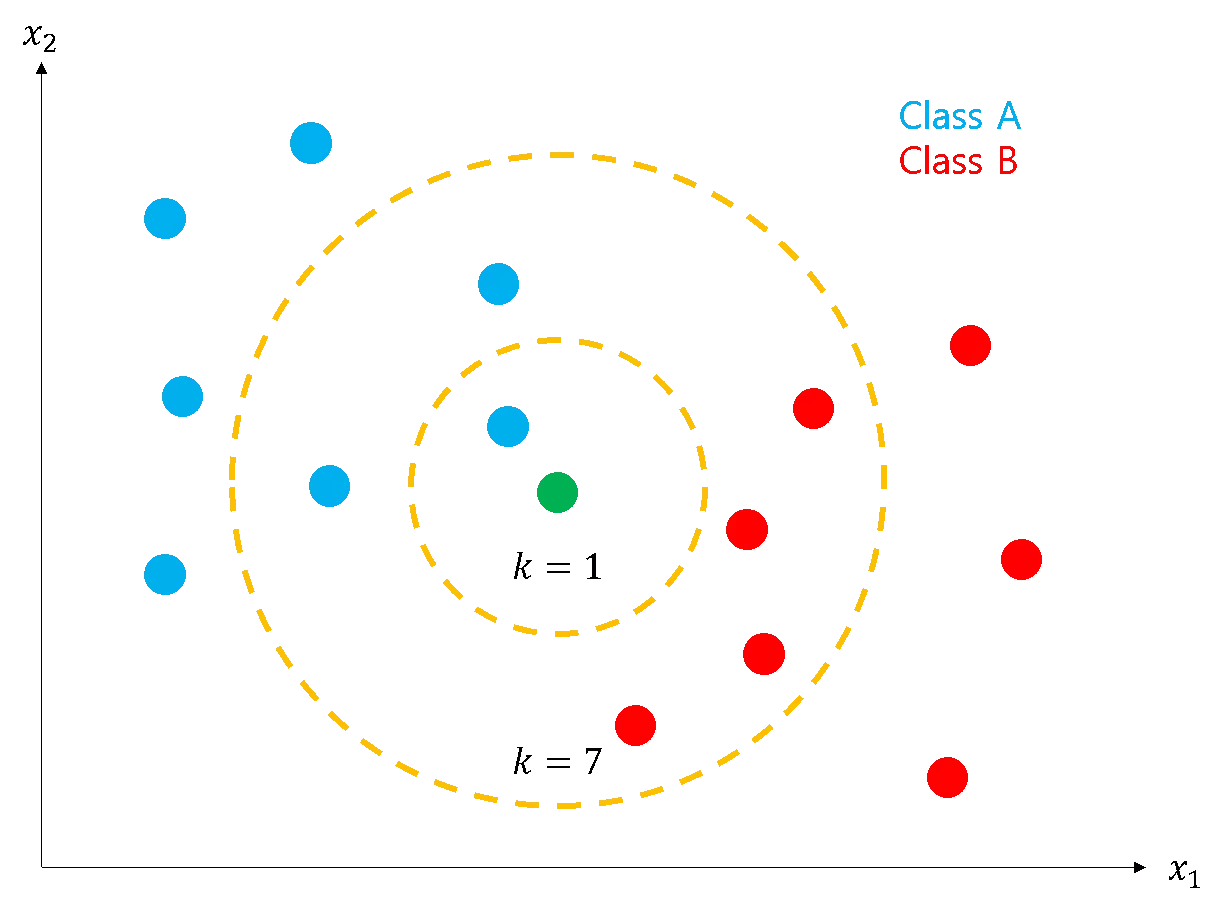
k-최근접 이웃(k-Nearest Neighbors): 기하 거리를 규칙으로 하여 관측치를 분류하는 알고리즘
\[\hat{y}=\text{arg} \max_{C}{\sum_{i=1}^{k}{I(y_{i}=C)}}\]
Distance
-
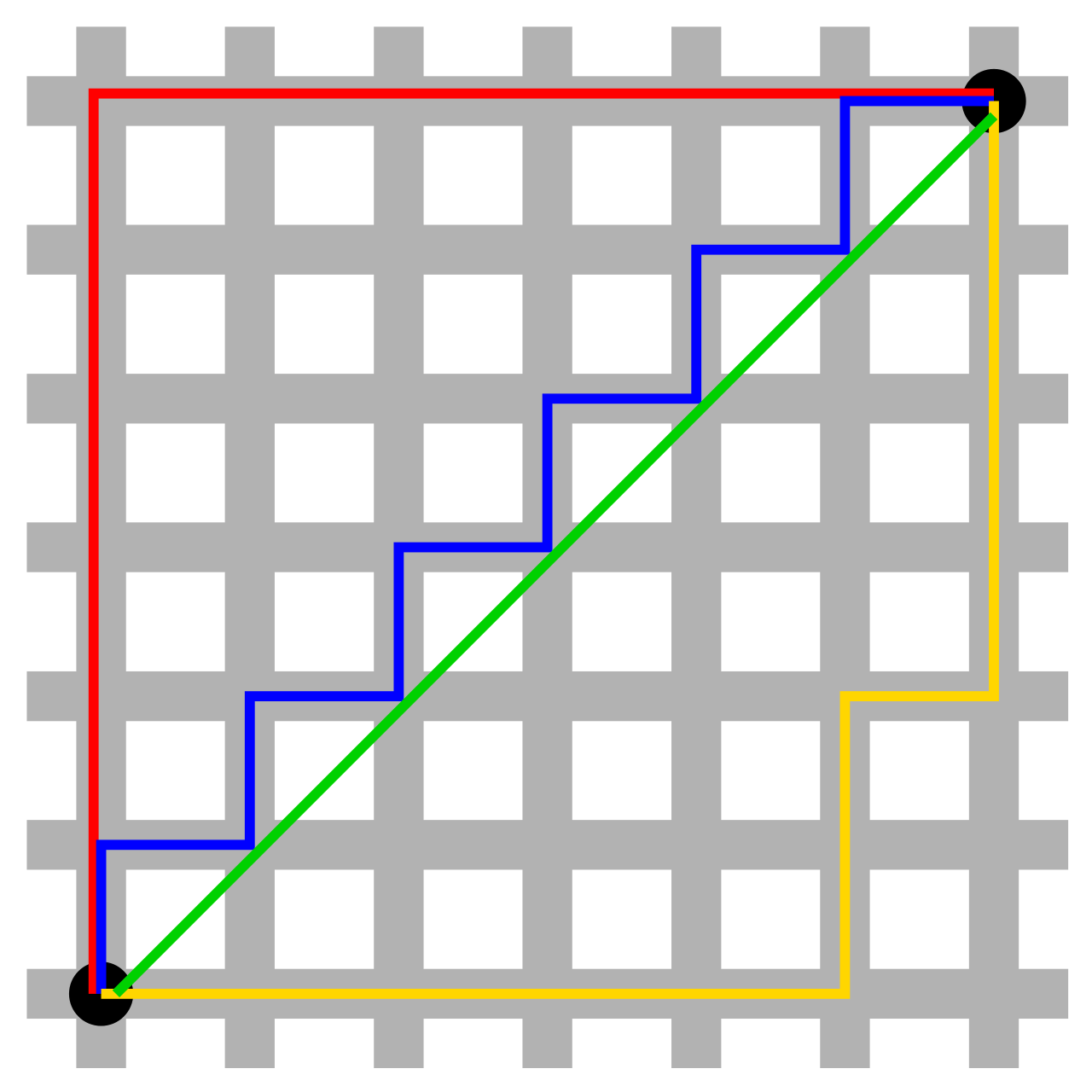
맨해튼 거리(Manhattan Distance; L1): 두 점 사이의 엣지(Edge) 갯수
\[\begin{aligned} \mathrm{d}(\mathbf{a},\mathbf{b}) = \Vert \mathbf{a} - \mathbf{b} \Vert _{L1} = \sum_{i=1}^{n}{\vert a_i - b_i \vert} \end{aligned}\]- \(\mathbf{e}_{1}, \mathbf{i}_{2}, \cdots, \mathbf{e}_{n}\) 를 기저벡터로 사용하는 $n$ 차원 좌표계에 위치한 두 벡터 $\mathbf{a}, \mathbf{b}$ 에 대하여 각 축 방향으로의 기저벡터 단위 거리를 합산한 값
-
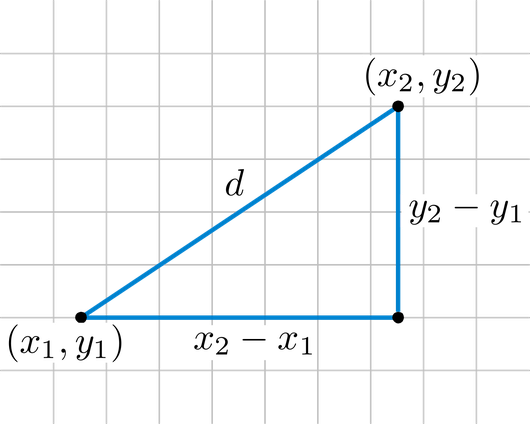
유클리드 거리(Euclidean Distance; L2): 두 점 사이의 직선 거리
\[\begin{aligned} \mathrm{d}(\mathbf{a},\mathbf{b}) = \Vert \mathbf{a} - \mathbf{b} \Vert _{L2} = \sqrt{\sum_{i=1}^{n}{(a_i - b_i)^{2}}} \end{aligned}\]- \(\mathbf{e}_{1}, \mathbf{e}_{2}, \cdots, \mathbf{e}_{n}\) 를 기저벡터로 사용하는 $n$ 차원 좌표계에 위치한 두 벡터 \(\mathbf{a}, \mathbf{b}\) 에 대하여 각 축 방향으로의 기저벡터 단위 거리의 제곱을 합산한 후 제곱근한 값
-
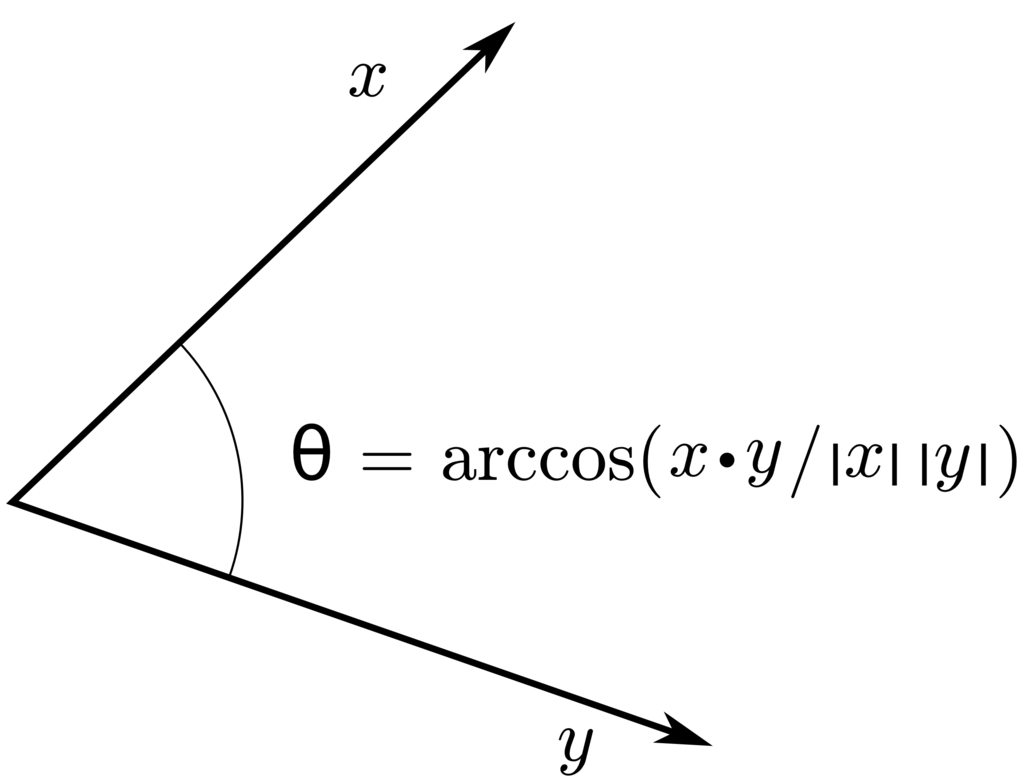
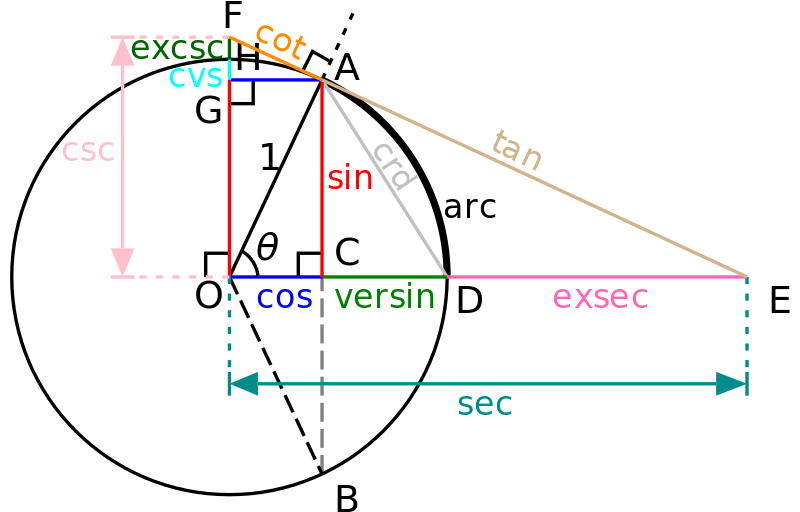
코사인 거리(Cosine Distance; $\cos$): 임의의 두 점에 대하여, 원점과 각 점을 잇는 직선의 사이각 $\theta$ 의 코사인 값
\[\begin{aligned} \mathrm{d}(\mathbf{a},\mathbf{b}) = \cos{\theta} = \frac{\mathbf{a}^{T}\mathbf{b}}{\Vert \mathbf{a} \Vert \cdot \Vert \mathbf{b} \Vert} = \frac{\sum_{i=1}^{n}{a_{i}b_{i}}}{\sqrt{\sum_{i=1}^{n}{a_{i}^{2}}} \cdot \sqrt{\sum_{i=1}^{n}{b_{i}^{2}}}} \end{aligned}\] -
하버사인 거리(Haversine Distance; $\text{hav}$): 구 표면상에 존재하는 두 지점에 대하여, 위도($\varphi$), 경도($\lambda$) 및 호 중심각($\Theta$)을 활용하여 측정한 호의 길이
-
반지름이 $r$, 호 $\overline{AB}$ 의 중심각이 $\Theta$ 일 때, 호 $\overline{AB}$ 의 길이 $d(A,B)$ 는 다음과 같음
\[\begin{aligned} d(A,B) &= r \cdot \Theta \end{aligned}\] -
점 $A$,$B$ 의 위도가 $\varphi_{A}$,$\varphi_{B}$, 경도가 $\lambda_{A}$,$\lambda_{B}$ 이고, 호 $\overline{AB}$ 의 중심각이 $\Theta$ 일 때, 호의 길이 $\text{hav}{\Theta}$ 는 다음과 같음
\[\begin{aligned} \text{hav}{\Theta} &= \text{hav}(\varphi_{B}-\varphi_{A}) + \cos{\varphi_{A}} \cdot \cos{\varphi_{B}} \cdot \text{hav}(\lambda_{B}-\lambda_{A}) \end{aligned}\] -
$\sin$, $\cos$, $\text{hav}$ 의 관계는 다음과 같음
\[\begin{aligned} \text{hav}{\Theta} &= \sin^{2}{\frac{\Theta}{2}}\\ &= \frac{1-\cos{\Theta}}{2} \end{aligned}\] -
따라서 반지름, 경도, 위도가 주어졌을 때 호 $\overline{AB}$ 의 길이 $d(A,B)$ 는 다음과 같음
\[\begin{aligned} d(A,B) &= r \cdot \Theta\\ &= r \cdot \text{archav}(\text{hav}{\Theta})\\ &= 2r \cdot \arcsin(\sqrt{\text{hav}{\Theta}})\\ &= 2r \cdot \arcsin\left(\sqrt{\text{hav}(\varphi_{B}-\varphi_{A}) + \cos{\varphi_{A}} \cdot \cos{\varphi_{B}} \cdot \text{hav}(\lambda_{B}-\lambda_{A})}\right) \end{aligned}\]
-
Sourse
- https://076923.github.io/posts/Python-opencv-43/