Qualitative Predictors

Level 2

---

어느 신용카드 사에서 고객이 학생인지 여부에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 학생인 사람의 신용카드 대금 평균
  • $\beta_1$ : 학생인 사람과 학생이 아닌 사람의 신용카드 대금 평균 차이

Level 3

---

어느 신용카드 사에서 고객의 인종(황인/흑인/백인)에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• 지시 변수(Indicate Variable)

  \[d_{1}^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if Black}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\\ \quad d_{2}^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if White}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d_{1}^{(i)} + \beta_{2} \cdot d_{2}^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if Black}\\ \beta_{0} + \beta_{2} + \varepsilon^{(i)} \quad &\text{if White}\\ \beta_{0} + \varepsilon^{(i)} \quad &\text{if Asian} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 황인의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 흑인의 신용카드 대금 평균
  • $\beta_1$ : 황인과 흑인의 신용카드 대금 평균 차이
  • $\beta_0 + \beta_2$ : 백인의 신용카드 대금 평균
  • $\beta_2$ : 황인과 백인의 신용카드 대금 평균 차이

Qualitative & Quantitative

---

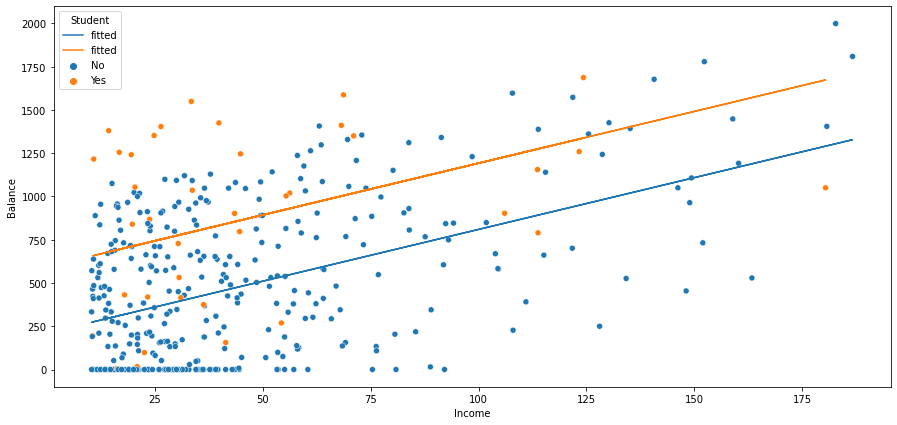
어느 신용카드 사에서 고객의 신용카드 대금에 관한 회귀 모형을 설계하고자 한다. 고객의 수입과 학생 여부에 관한 데이터를 확보하고 있다.

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ 0 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} + \beta_{2} \cdot x^{(i)} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 참조 수준(Reference Level) 으로서 $x$(Income)이 동일한 수준일 때 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : $x$(Income)이 동일한 수준일 때 학생인 사람의 신용카드 대금 평균
  • $\beta_1$ : $x$(Income)이 동일한 수준일 때 학생인 사람과 학생이 아닌 사람의 신용카드 대금 평균 차이
  • $\beta_2$ : 학생 여부와 무관하게, $x$(Income) 단위 변동에 따른 $y$ 의 변동성

Effect Coding

---

어느 신용카드 사에서 고객이 학생인지 여부에 따른 신용카드 대금에 관한 회귀 모형을 설계하고자 한다.

• Effect Coding : 각 범주의 효과를 비교하기 위하여 참조 수준을 명시적으로 사용하지 않고 전체 평균과 비교하는 범주형 변수 인코딩 방법

• 지시 변수(Indicate Variable)

  \[d^{(i)} = \begin{cases}\begin{aligned} 1 \quad &\text{if student}\\ -1 \quad &\text{otherwise} \end{aligned}\end{cases}\]

• 선형 회귀 모형

  \[\begin{aligned} y^{(i)} &= \beta_{0} + \beta_{1} \cdot d^{(i)} + \varepsilon^{(i)}\\ &= \begin{cases}\begin{aligned} \beta_{0} + \beta_{1} + \varepsilon^{(i)} \quad &\text{if student}\\ \beta_{0} - \beta_{1} + \varepsilon^{(i)} \quad &\text{otherwise} \end{aligned}\end{cases} \end{aligned}\]
  • $\beta_0$ : 모든 사람들의 신용카드 대금 평균
  • $\beta_0 + \beta_1$ : 학생인 사람의 신용카드 대금 평균
  • $\beta_0 - \beta_1$ : 학생이 아닌 사람의 신용카드 대금 평균
  • $\beta_1$ : 학생 여부에 따른 신용카드 대금 평균의 차이