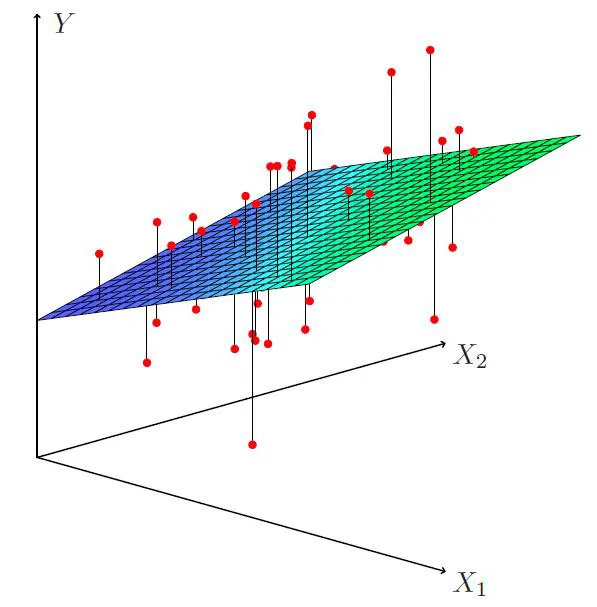
Regression Coefficient Estimation

Ordinary Least Squares

---

• 최소자승법(Ordinary Least Squares; OLS) : 잔차 자승의 합을 최소화하는 회귀계수를 추정하는 방법

  \[\begin{aligned} \hat{\beta}_{0}, \hat{\beta}_{1} &= \text{arg} \min_{\theta}{\sum_{i=1}^{n}{\varepsilon_{i}^{2}}}\\ &= \text{arg} \min_{\theta}{\sum_{i=1}^{n}{\left(y_{i} - \hat{y}_{i} \right)^{2}}}\\ &= \text{arg} \min_{\theta}{\sum_{i=1}^{n}{\left[ y_{i} - \left(\beta_{0} + \beta_{1} x_{i} \right) \right]^2}} \end{aligned}\]

• $\mathcal{L}(\beta_{0}, \beta_{1})=\displaystyle\sum_{i=1}^{n}{\varepsilon_{i}^{2}}$ 을 $\beta_{0}$ 으로 편미분

  \[\begin{aligned} &\frac{\partial}{\partial \beta_{0}}\mathcal{L}(\beta_{0}, \beta_{1})\\ &= -2 \times \sum_{i=1}^{n}{\left[y_{i}-\left(\beta_{0} + \beta_{1} x_{i}\right)\right]} \\ &= -2 \times \left[\sum_{i=1}^{n}{y_{i}} - n \beta_{0}-\beta_{1} \sum_{i=1}^{n}{x_{i}} \right] \cdots ①\\ &= -2n \times (\overline{Y} - \beta_{0} - \beta_{1} \overline{X}) \\ &= 0 \end{aligned}\]

• 편향 $\beta_{0}$ 의 최소자승추정량 $\hat{\beta}_{0}$ 도출

  \[\therefore \hat{\beta_0} = \overline{Y} - \hat{\beta_1}\overline{X} \quad (\text{s.t.} \; n \ne 0)\]

• $\mathcal{L}(\beta_{0}, \beta_{1})=\displaystyle\sum_{i=1}^{n}{e_{i}^{2}}$ 을 $\beta_0$ 으로 편미분

  \[\begin{aligned} &\frac{\partial}{\partial \beta_{1}} \mathcal{L}(\beta_{0}, \beta_{1})\\ &= -2\times\sum_{i=1}^{n}{\left[y_{i}-\left(\beta_{0} + \beta_{1} x_{i}\right)\right] \times x_{i}}\\ &= -2\times\left[\sum_{i=1}^{n}{y_{i}x_{i}}-\beta_0\sum_{i=1}^{n}{x_{i}}-\beta_{1}\sum_{i=1}^{n}{x_{i}^{2}}\right] \cdots ② \\ &= 0 \end{aligned}\]

• 식 $①$ 변형

  \[\begin{aligned} & -\frac{1}{2} \times ① \times \sum_{i=1}^{n}{x_{i}}\\ &= \sum_{i=1}^{n}{x_{i}} \sum_{i=1}^{n}{x_{i}} - n \beta_{0} \sum_{i=1}^{n}{x_{i}} - \beta_{1} \sum_{i=1}^{n}{x_{i}} \sum_{i=1}^{n}{x_{i}}\\ &= n^{2}\overline{Y}\overline{X} - n^{2}\beta_{0}\overline{X}-n^{2}\beta_{1}\left(\overline{X}\right)^{2}\\ &= 0 \end{aligned}\]

• 식 $②$ 변형

  \[\begin{aligned} & -\frac{1}{2} \times ② \times n \\ &= n \sum_{i=1}^{n}{y_{i}x_{i}} - n \beta_0 \sum_{i=1}^{n}{x_{i}} - n \beta_{1} \sum_{i=1}^{n}{(x_{i})^{2}}\\ &= n \sum_{i=1}^{n}{y_{i}x_{i}} - n^{2} \beta_0 \overline{X} - n \beta_{1} \sum_{i=1}^{n}{x_{i}^{2}}\\ &= 0 \end{aligned}\]

• 식 ①, ② 의 변형을 뺄셈

  \[\begin{aligned} & -\frac{1}{2} \left(① \times \sum_{i=1}^{n}X_{i} - ② \times n \right)\\ &= \left[n^{2}\overline{Y}\overline{X} - n^{2}\beta_{1}\left(\overline{X}\right)^{2}\right] - \left[n \sum_{i=1}^{n}{y_{i}x_{i}} - n \beta_1 \sum_{i=1}^{n}{(x_{i})^{2}}\right]\\ &= \beta_{1} \times n^{2}\left[\frac{1}{n}\sum_{i=1}^{n}{x_{i}^{2}}-\left(\overline{X}\right)^{2}\right] - n^{2}\left[\frac{1}{n}\sum_{i=1}^{n}{y_{i}x_{i}}-\overline{Y}\overline{X}\right]\\ &= \beta_{1} \times n^{2} \mathrm{Var}\left[X\right] - n^{2} \mathrm{Cov}\left[Y,X\right]\\ &= 0 \end{aligned}\]

• 가중치 $\beta_{1}$ 의 최소자승추정량 $\hat{\beta}_{1}$ 도출

  \[\begin{aligned} \hat{\beta}_{1} &= \frac{\mathrm{Cov}\left[Y,X\right]}{\mathrm{Var}\left[X\right]} \end{aligned}\]

Gauss-Markov Assumptions

---

• A.1 반응변수의 선형 조건부 기대값 가정

  \[\mathbb{E}\left[y\mid X\right]=X\beta\]

• A.2 오차항의 등분산성(Homoskedasticity) 가정

  \[\mathrm{Var}\left[\varepsilon_i \mid X\right]=\sigma^2,\quad \forall i=1,\cdots,n\]

• A.3 오차항의 자기상관 없음(No Autocorrelation) 가정

  \[\mathrm{Cov}\left[\varepsilon_i, \varepsilon_j\mid X\right]=0,\quad i\ne j\]

• A.4 오차항의 정규성(Normality) 가정

  \[\varepsilon\mid\mathbf{X}\sim\mathcal{N}(0,\sigma^{2})\]

• A.5 설명변수 간 선형 독립(Linear Independence) 가정

  \[\mathrm{rank}(X)=p,\quad X\in\mathbb{R}^{n\times p}\]

OLS $\hat{\beta}_{1}$ subject to Gauss-Markov Assumptions

---

• 가중치 $\beta_{1}$ 의 최소자승추정량 $\hat{\beta}_{1}$ 은 $Y$ 의 선형 결합임

  \[\begin{aligned} \hat{\beta}_{1} &= \frac{\mathrm{Cov}\left[Y,X\right]}{\mathrm{Var}\left[X\right]}\\ &= \frac{\sum_{i=1}^{n}(x_{i}-\overline{x})(y_{i}-\overline{y})}{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}\\ \\ \sum_{i=1}^{n}{(x_{i}-\overline{x})(y_{i}-\overline{y})} &= \sum_{i=1}^{n}{(x_{i}-\overline{x}) \cdot y_{i}} - \sum_{i=1}^{n}{(x_{i}-\overline{x}) \cdot \overline{y}}\\ &= \sum_{i=1}^{n}{(x_{i}-\overline{x}) \cdot y_{i}} - \overline{y} \cdot \sum_{i=1}^{n}{(x_{i}-\overline{x})}\\ &= \sum_{i=1}^{n}{(x_{i}-\overline{x}) \cdot y_{i}}\\ \\ \therefore \hat{\beta}_{1} &= \sum_{i=1}^{n}{\underbrace{\frac{(x_{i}-\overline{x})}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}}}_{=:w_{i}}}\cdot y_{i}\\ &= w_{1} \cdot y_{1} + w_{2} \cdot y_{2} + \cdots + w_{n} \cdot y_{n} \end{aligned}\]

• $\sum_{i=1}^{n}{w_{i}}=0$

  \[\begin{aligned} \sum_{i=1}^{n}{w_{i}} &=\sum_{i=1}^{n}{\frac{(x_{i}-\overline{x})}{\sum_{j=1}^{n}{(x_j-\overline{x})^2}}}\\ &=\frac{1}{\sum_{j=1}^{n}{(x_j-\overline{x})^2}}\cdot\left(\sum_{i=1}^{n}{(x_{i}-\overline{x})}\right)\\ \\ \sum_{i=1}^{n}{(x_{i}-\overline{x})} &=\sum_{i=1}^{n}{x_{i}}-n\cdot\overline{x}\\ &=n\cdot\overline{x}-n\cdot\overline{x}\\ &=0\\ \\ \therefore \sum_{i=1}^{n}{w_{i}} &=\frac{1}{\sum_{j=1}^{n}{(x_j-\overline{x})^2}}\cdot 0\\ &=0 \end{aligned}\]

• $\sum_{i=1}^{n}{w_{i} \cdot x_{i}}=1$

  \[\begin{aligned} \sum_{i=1}^{n}{w_{i} \cdot x_{i}} &= \sum_{i=1}^{n}{\frac{(x_{i}-\overline{x})}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}} \cdot x_{i}}\\ &= \frac{\sum_{i=1}^{n}{(x_{i}-\overline{x})\cdot x_{i}}}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}}\\ \\ \sum_{i=1}^{n}{(x_{i}-\overline{x})\cdot x_{i}} &= \sum_{i=1}^{n}{(x_{i}^{2}-\overline{x}\cdot x_{i})}\\ &= \sum_{i=1}^{n}{x_{i}^{2}} - \overline{x}\cdot\sum_{i=1}^{n}{x_{i}}\\ &= \sum_{i=1}^{n}{x_{i}^{2}} - n\cdot \overline{x}^{2}\\ &= \sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}\\ \\ \therefore \sum_{i=1}^{n}{w_{i} \cdot x_{i}} &= \frac{\sum_{i=1}^{n}{(x_{i}-\overline{x})\cdot x_{i}}}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}}\\ &= \frac{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}}\\ &= 1 \end{aligned}\]

• $\sum_{i=1}^{n}{w_{i}^{2}}=\displaystyle\frac{1}{\sum_{i=1}^{n}(x_{i}-\overline{x})^{2}}$

  \[\begin{aligned} \sum_{i=1}^{n}{w_{i}^{2}} &= \sum_{i=1}^{n}{\left(\frac{(x_{i}-\overline{x})}{\sum_{j=1}^{n}(x_{j}-\overline{x})^{2}}\right)^{2}}\\ &= \frac{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}{\left(\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}\right)^{2}}\\ &= \frac{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}} \cdot \sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}}\\ &= \frac{1}{\sum_{j=1}^{n}{(x_{j}-\overline{x})^{2}}} \end{aligned}\]

• 따라서 최소자승추정량 \(\hat{\beta}_{1}\) 과 그 모수 \(\beta_{1}\) 사이에는 다음이 성립함

  \[\begin{aligned} \hat{\beta}_{1} &= \sum_{i=1}^{n}{w_{i} \cdot y_{i}}\\ &= \sum_{i=1}^{n}{w_{i} \cdot (\beta_{0}+\beta_{1} \cdot x_{i}+\varepsilon_{i})}\\ &= \beta_{1} + \sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}} \end{aligned}\]

Gauss-Markov Theorem

---

고전적 선형 회귀 가정(Classical Linear Regression Assumptions or Gauss-Markov Assumptions) 하 최소자승추정량은 선형 불편 추정량 중 분산이 가장 작은 추정량(Best Linear Unbiased Estimator; BLUE)이다.

• 가중치 $\beta_{1}$ 의 최소자승추정량 $\hat{\beta}_{1}$ 의 확률분포

  \[\hat{\beta}_{1} \sim N\left(\beta_{1}, \sigma^{2}\left[\displaystyle\frac{1}{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}\right]\right)\]

• 편향 $\beta_{0}$ 의 최소자승추정량 $\hat{\beta}_{0}$ 의 확률분포

  \[\hat{\beta}_{0} \sim N\left(\beta_{0}, \sigma^{2} \left[\displaystyle\frac{1}{n} + \displaystyle\frac{\overline{x}^{2}}{\sum_{i=1}^{n}{(x_{i}-\overline{x})^{2}}}\right]\right)\]

• 오차항 $\varepsilon$ 의 모분산 $\sigma^{2}$ 을 그 표본분산으로 추정함

  \[\sigma^{2} \xrightarrow{P} \frac{\text{RSS}}{n-2}\]

OLS is Unbiased Estimator

• 고전적 선형 회귀 가정 하 $\beta_1$ 의 최소자승추정량 $\hat{\beta}_{1}$ 의 기대값은 다음과 같음

  \[\begin{aligned} \mathbb{E}\left[\hat{\beta}_{1}\right] &= \mathbb{E}\left[\beta_{1} + \sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}}\right]\\ &= \mathbb{E}\left[\beta_{1}\right] + \mathbb{E}\left[\sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}}\right]\\ &= \beta_{1} + \mathbb{E}\left[\sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}}\right]\\ &= \beta_{1} + \sum_{i=1}^{n}{\mathbb{E}\left[w_{i} \cdot \varepsilon_{i}\right]} \end{aligned}\]

• $\because\mathbb{E}\left[\varepsilon_i \mid X\right]=0$

  \[\begin{aligned} \mathbb{E}\left[\hat{\beta}_{1}\right] &= \beta_{1} + \sum_{i=1}^{n}{\mathbb{E}\left[w_{i}\right] \cdot \mathbb{E}\left[\varepsilon_{i}\right]}\\ &= \beta_{1} + \sum_{i=1}^{n}{\mathbb{E}\left[w_{i}\right] \cdot 0}\\ &= \beta_{1} \end{aligned}\]

• 따라서 고전적 선형 회귀 가정 하 최소자승추정량 $\hat{\beta}_1$ 은 $\beta_1$ 의 불편 추정량임

  \[\begin{aligned} \therefore \mathrm{Bias}\left[\hat{\beta}_{1}\right] &= \mathbb{E}\left[\hat{\beta}_{1}\right] - \beta_{1}\\ &= 0 \end{aligned}\]

OLS is Efficient Estimator

• $\beta_{1}$ 의 최소자승추정량 $\hat{\beta}_{1}$ 의 분산은 다음과 같음

  \[\begin{aligned} \mathrm{Var}\left[\hat{\beta}_{1}\right] &= \mathrm{Var}\left[\beta_{1} + \sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}}\right]\\ &= \mathrm{Var}\left[\sum_{i=1}^{n}{w_{i} \cdot \varepsilon_{i}}\right]\\ &= \sum_{i=1}^{n}{w_{i}^{2} \cdot \sigma_{i}^{2}} + \sum_{i}\sum_{j \ne i}{w_{i} \cdot w_{j} \cdot \mathrm{Cov}\left[\varepsilon_{i}, \varepsilon_{j}\right]} \end{aligned}\]

• $\because \mathrm{Cov}\left[\varepsilon_{i}, \varepsilon_{j}\mid X\right]=0$

  \[\begin{aligned} \mathrm{Var}\left[\hat{\beta}_{1}\right] &= \sum_{i=1}^{n}{w_{i}^{2} \cdot \sigma_{i}^{2}} \end{aligned}\]

• $\because \sigma_{i^{\forall}}^{2}=\sigma^{2}$

  \[\begin{aligned} \mathrm{Var}\left[\hat{\beta}_{1}\right] &= \sigma^{2} \cdot \sum_{i=1}^{n}{w_{i}^{2}} \end{aligned}\]

• 따라서 고전적 선형 회귀 가정 하 $\hat{\beta}_1$ 은 $\beta_1$ 의 불편 추정량 중 분산이 가장 작은 추정량임

  \[\sigma^{2} \cdot \sum_{i=1}^{n}{w_{i}^{2}} \le \sum_{i=1}^{n}{w_{i}^{2} \cdot \sigma_{i}^{2}} + \sum_{i}\sum_{j \ne i}{w_{i} \cdot w_{j} \cdot \mathrm{Cov}\left[\varepsilon_{i}, \varepsilon_{j}\right]}\]

---

Sourse

• https://medium.com/@luvvaggarwal2002/linear-regression-in-machine-learning-9e8af948d3eb