Regression Diagnostics (1) Nonlinearity

Regression Diagnostics

---

• A.1 반응변수와 설명변수 간 비선형성 문제(Non-Linearity Problem): 반응변수의 조건부 기대값이 설명변수들의 선형 결합 형태가 아님에 따라 계수 벡터의 최소자승추정량이 불편추정량이 될 수 없는 문제

  \[\cancel{\exists}\beta\in\mathbb{R}^{P} \quad\mathrm{s.t.}\quad \mathbb{E}\left[\mathbf{y}\mid\mathbf{X}\right] =\mathbf{X}\beta\]

• A.2 오차항의 이분산성 문제(Hetero-Scedasticity Problem): 오차항의 등분산 가정이 위배됨에 따라 계수 벡터의 최소자승추정량이 효율추정량이 될 수 없는 문제

  \[\exists i\ne j:\mathrm{Var}\left[\varepsilon_{i}\mid\mathbf{X}\right]\ne\mathrm{Var}\left[\varepsilon_{j}\mid\mathbf{X}\right]\\ \Updownarrow\\ \mathrm{Var}\left[\varepsilon\mid\mathbf{X}\right] =\mathrm{diag}(\sigma_{1}^{2},\cdots,\sigma_{N}^{2})\ne\sigma^{2}\mathbf{I}\]

• A.3 오차항의 자기상관 문제(Auto-Correlation Problem): 오차항의 자기상관이 존재함에 따라 계수 벡터의 최소자승추정량이 효율추정량이 될 수 없는 문제

  \[\exists i\ne j:\mathrm{Cov}\left[\varepsilon_{i},\varepsilon_{j}\mid \mathbf{X}\right]\ne 0 \quad\Longleftrightarrow\quad \mathrm{Var}\left[\varepsilon\mid\mathbf{X}\right]\ne\sigma^{2}\mathbf{I}\]

• A.5 설명변수 간 다중공선성 문제(Multi-Col-Linearity Problem): 설명변수들이 선형 종속됨에 따라 계수 벡터가 유일하게 결정되지 못하는 문제

  \[\mathrm{rank}(\mathbf{X})\ne p \quad\mathrm{for}\quad\mathbf{X}\in\mathbb{R}^{N\times P}\]

Non-Linearity Problem

---

• 반응변수의 조건부 기대값이 설명변수에 대한 함수라고 하자:

  \[\begin{gathered} \mathbb{E}\left[\mathbf{y}\mid\mathbf{X}\right] =f(\mathbf{X})\\ \Updownarrow\\ \mathbf{y}=f(\mathbf{X})+\varepsilon,\quad\varepsilon\sim\mathcal{N}(0,\sigma^{2}) \end{gathered}\]

• 선형 회귀 모형:

  \[\begin{aligned} \hat{\mathbf{y}} &=\mathbf{X}\hat{\beta} \end{aligned}\]

• 조건부 기대값의 모형 편향:

  \[\begin{aligned} \mathbb{E}\left[\mathbf{y}\mid\mathbf{X}\right]-\mathbb{E}\left[\hat{\mathbf{y}}\mid\mathbf{X}\right] &=f(\mathbf{X})-\mathbb{E}\left[\mathbf{X}\hat{\beta}\mid\mathbf{X}\right]\\ &=f(\mathbf{X})-\mathbf{X}\cdot\mathbb{E}\left[\hat{\beta}\mid\mathbf{X}\right]\\ &=f(\mathbf{X})-\mathbf{X}\beta \end{aligned}\]

• 함수 $f$ 가 설명변수의 선형 결합이 아닐 경우 선형 회귀 모형의 적합값은 조건부 기대값의 불편추정량이 될 수 없음:

  \[f(\mathbf{X})-\mathbf{X}\beta\ne 0\]

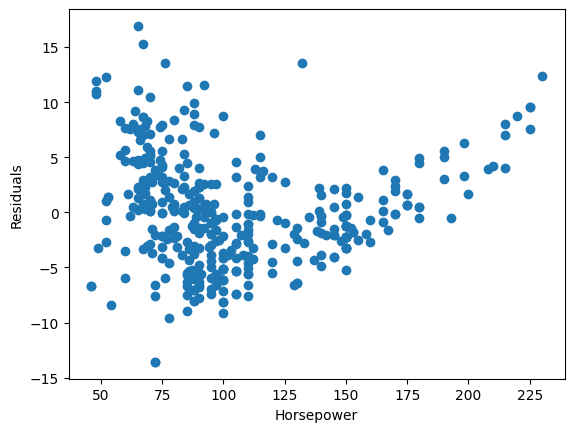
• 잔차 $\epsilon$ 의 그래프가 $0$ 을 중심으로 무작위하게 분포하지 않고 체계적인 패턴을 보이는 경우 선형성 가정이 위배되었다고 진단함:

  \[\begin{aligned} \epsilon &=\mathbf{y}-\hat{\mathbf{y}}\\ &=f(\mathbf{X})+\varepsilon-\mathbf{X}\hat{\beta}\\ \mathbb{E}\left[\epsilon\mid\mathbf{X}\right] &=f(\mathbf{X})-\mathbf{X}\beta\\ &\ne 0 \end{aligned}\]

Box-Cox Transformation

---

• 반응변수와 설명변수가 단조(monotone) 관계이나 증감 속도가 왜곡되어(스케일이 뒤틀려서) 비선형성을 띠게 되었다고 가정하자:

  \[\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}x}f(x)>0, \quad\frac{\mathrm{d}^{2}}{\mathrm{d}x^{2}}f(x)\ne0 \end{aligned}\]

• 증감 속도를 보정하는 비선형 링크 함수 $h$ 가 존재한다면 그 역함수를 통해 반응변수를 변환함으로써 조건부 기대값의 선형 가정을 만족할 수 있음:

  \[\begin{gathered} \mathbb{E}\left[\mathbf{y}\mid\mathbf{X}\right] =f(\mathbf{X}) =h(\mathbf{X}\beta)\\ \Updownarrow\\ \mathbb{E}\left[h^{-1}(\mathbf{y})\mid\mathbf{X}\right] =\mathbf{X}\beta \end{gathered}\]

• 박스-콕스 변환(Box-Cox Transformation): 반응변수에 적용되는 단조 멱변환으로서 조건부 기대값의 스케일 왜곡을 우도 기반으로 교정하여 선형 회귀 가정을 만족시키도록 하는 변수 변환

  \[z =\begin{cases} \left(y^{\lambda}-1\right)/\lambda,\quad&\lambda\ne0\\ \log{y},\quad&\lambda=0 \end{cases} \quad\mathrm{s.t.}\quad \forall y >0\]

• likelihood function:

  \[\begin{aligned} p_{y}(\mathbf{y})\mathrm{d}\mathbf{y} &=p_{z}(\mathbf{z})\mathrm{d}\mathbf{z}\\ \therefore p_{y}(\mathbf{y}) &=p_{z}(\mathbf{z})\left\vert\frac{\mathrm{d}\mathbf{z}}{\mathrm{d}\mathbf{y}}\right\vert\\ &=\mathcal{N}(\mathbf{X}\beta,\sigma^{2})\cdot\prod_{i=1}^{N}{y_{i}^{\lambda-1}} \end{aligned}\]

• log likelihood function:

  \[\mathcal{L}(\lambda,\theta) =-\frac{2}{n}\log{2\pi}-\frac{2}{n}\log{\sigma^{2}}-\frac{1}{2\sigma^{2}}\Vert\mathbf{z}-\mathbf{X}\beta\Vert^{2}+(\lambda-1)\sum_{i=1}^{N}{\log{y_{i}}}\]

• optimization:

  \[\begin{aligned} \hat{\lambda} &=\mathrm{arg}\max_{\lambda}\max_{\theta}{\mathcal{L}(\theta,\lambda)}\quad\mathrm{for}\quad\theta=(\beta,\sigma^{2}) \end{aligned}\]