Variational AutoEncoder

Variational AutoEncoder

---

• 불확실성(Uncertainty): 어떠한 사건에 대하여 확신할 수 없는 상태

  • 우발적 불확실성(Aleatoric Uncertainty): 관측치에 내재된 잡음 혹은 무작위성으로 인해 발생하는 불확실성

  • 인식적 불확실성(Epistemic Uncertainty): 정보 불완전성으로 인하여 발생하는 불확실성
    • 정보 불완전성(Data Uncertainty): 관측 데이터가 불완전하거나(Incomplete), 불충분하거나(Insufficient), 왜곡된(Distorted) 상황
    • 파라미터 불확실성(Parameter Uncertainty): 주어진 모형 안에서 최적 파라미터를 유일하게 식별할 수 없는 문제
    • 구조적 불확실성(Structural Uncertainty): 데이터 생성 메커니즘을 기술하는 함수 구조를 확신할 수 없어 특정 모형을 가정할 수 없는 문제
    • 표현의 불확실성(Latent Representation Uncertainty): 잠재공간의 비식별성으로 인해 치역(관측값)만으로 정의역(잠재요인)을 유일하게 결정하여 표현할 수 없는 문제
  • 존재론적 불확실성(Ontic Uncertainty): 모형이 모사하고자 하는 실제 메커니즘이 본질적으로 불확실하여 정보가 증가하더라도 제거될 수 없는 불확실성

• 문제 의식: 확률적 경사하강법을 적용하여 표현의 불확실성을 효율적으로 수행할 수 있는 일반적인 방법론이 부재함

  연속 잠재요인을 가지는 베이지안 모형에서 사후 분포는 대체로 비가해적임(Intractable). 즉, 해석적 표현이나 미분 가능한 형태의 표현을 구하기 어려움. 이를 근사하기 위한 몬테-카를로 시뮬레이션 기반 근사 방법은 역전파 학습을 적용할 수 없거나(MCMC), 분산이 매우 커서 추정이 불안정함(VI).

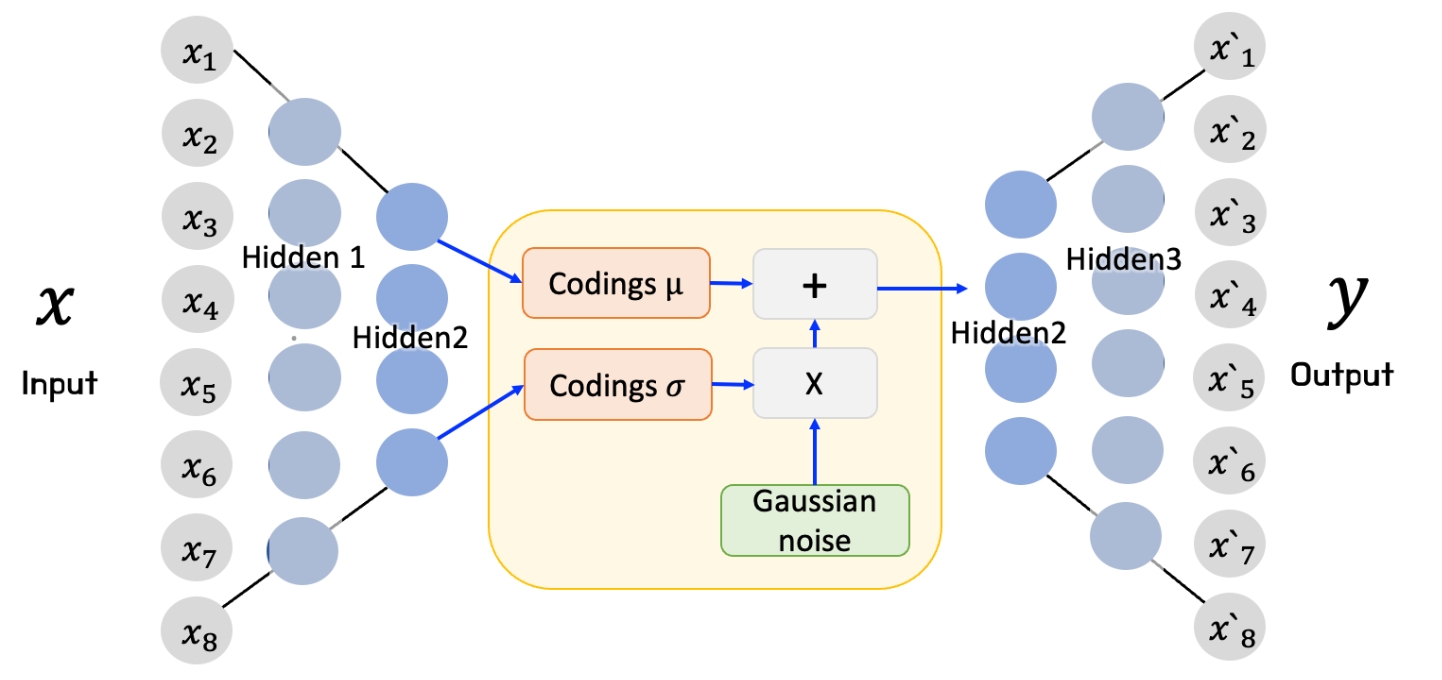
• 변분 오토인코더(Variational AutoEncoder; VAE) : 오토인코더 아키텍처의 잠재 공간을 확률변수화하여 표현의 불확실성을 모델링하되, 재매개변수화 트릭(Reparameterization Trick) 을 적용하여 잠재요인의 근사 분포(Encoder)와 우도(Decoder) 학습을 확률적 경사하강법(Stochastic Gradient Variational Bayes) 을 통해 수행하는 생성 모형(Generative Model)

  • Variational Inference
  • Reparameterization Trick

How to Modeling

---

Modified Architecture

\[\begin{gathered} X \xrightarrow{\text{Encoder}} Z \xrightarrow{\text{Decoder}} \hat{X}\\ \Downarrow\\ X \xrightarrow{\text{Encoder}} Q(Z \mid X) \xrightarrow{\text{Decoder}} P(X \mid Z) \end{gathered}\]

• encoder module, which reduces the obs $X \in \mathbb{R}^{N}$ to latent factor dimensions $Z \in \mathbb{R}^{M}(M\ll N)$, is approx. estimator:

  \[Z=F(X;\phi)\quad\Longrightarrow\quad Q\left(Z\mid X;\phi\right)\approx P(Z\mid X)\]

• latent space is approx. conditional on obs:

  \[Z\quad\Longrightarrow\quad Z\mid X\]

• decoder module, which reconstruct obs $\hat{X}$ from latent factor $Z$, is likelihood estimator:

  \[\hat{X}=G(Z;\theta)\quad\Longrightarrow\quad P\left(X\mid Z;\theta \right)\]

Stochastic Gradient Variational Bayes

• prior is multi-variate gaussian dist.:

  \[\begin{aligned} Z \sim \mathcal{N}(0,\sigma^{2}\mathbf{I})\quad\Leftrightarrow\quad Z_{i}\perp Z_{j} \end{aligned}\]

• posterior is approximated by latent space:

  \[\begin{aligned} P(Z \mid X) \propto \underbrace{P(X\mid Z)}_{\text{est. by decoder}}P(Z) \approx \underbrace{Q(Z \mid X)}_{\text{est. by encoder}} \end{aligned}\]

• Reparameterization Trick is a technique that transforms the sampling process from an approximate distribution into a differentiable function:

  \[\begin{gathered} Z_{i} \sim \mathcal{N}(\mu_{i},\sigma_{i}^{2})\\ \Downarrow\\ Z_{i} = \mu_{i} + \sigma_{i} \cdot \epsilon_{i}, \quad \epsilon_{i} \sim \mathcal{N}(0,1) \end{gathered}\]

• ELBO with reparameterization trick can be applied to stochastic gradient descent:

  \[\begin{aligned} \mathrm{ELBO} :=\mathbb{E}_{Z\sim Q}\left[\log{p(X\mid Z ; \theta)}\right]-D_{KL}\left[q(Z;\phi)\parallel p(Z)\right] \end{aligned}\]

---

Source

• https://velog.io/@jochedda/%EB%94%A5%EB%9F%AC%EB%8B%9D-Autoencoder-%EA%B0%9C%EB%85%90-%EB%B0%8F-%EC%A2%85%EB%A5%98